【小奥】问题11 九块耕地求面积

问题

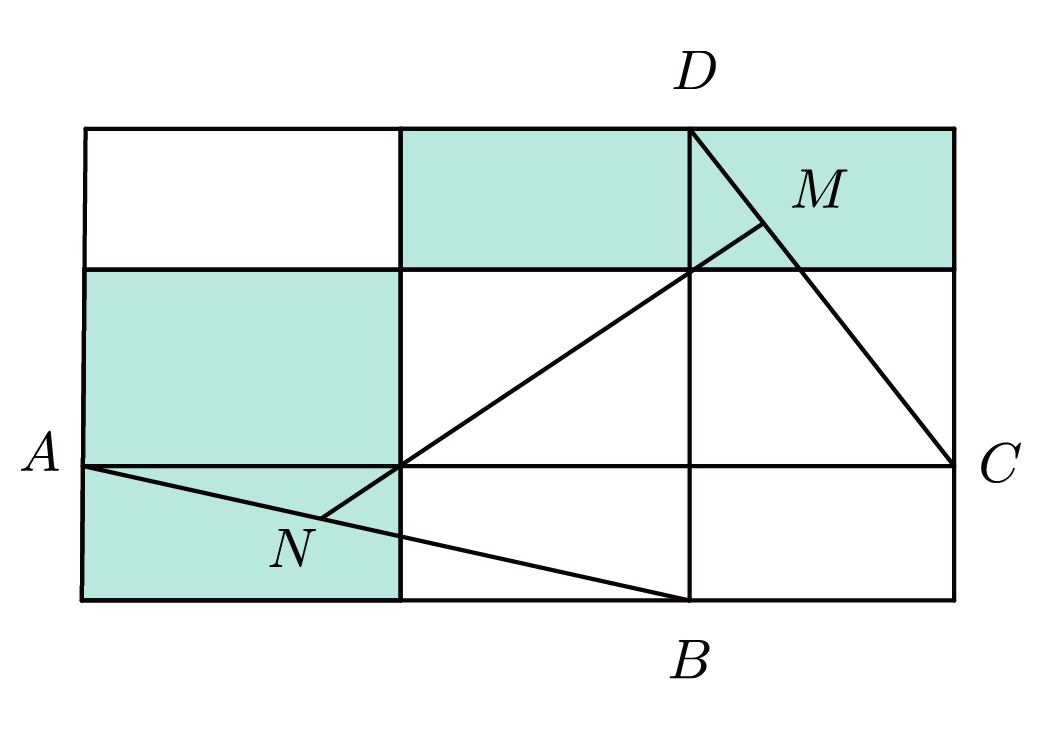
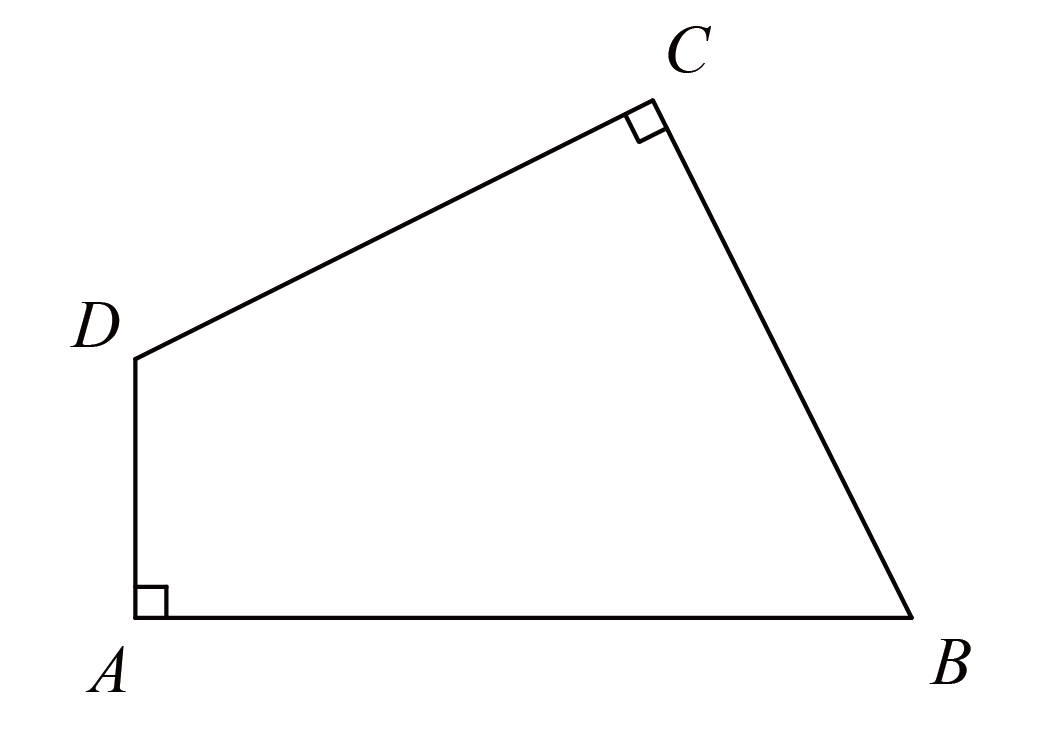
如图，一块耕地被分成了$9$块长方形的菜地，其中两块阴影的面积都是$18$．如果$MC=3DM$，$4AN=3NB$，那么，整块耕地的面积是多少？

解析

由梅涅劳斯定理可得：$$\frac{AN}{NB}\times \frac{BP}{PD}\times \frac{DM}{MC}\times \frac{CQ}{QA}=1$$

则$$\frac{BP}{PD}\times \frac{CQ}{QA}=4\Rightarrow BP\times CQ=4PD\times QA$$

即右下角面积为左上角面积的$4$倍，设左上角面积为$a$，则右下角面积为$4a$，因此

$$18\times 18 =a\times 4a$$

所以$a=9$，那么长方形面积为$9+18+18+36=81$．

梅涅劳斯定理简介

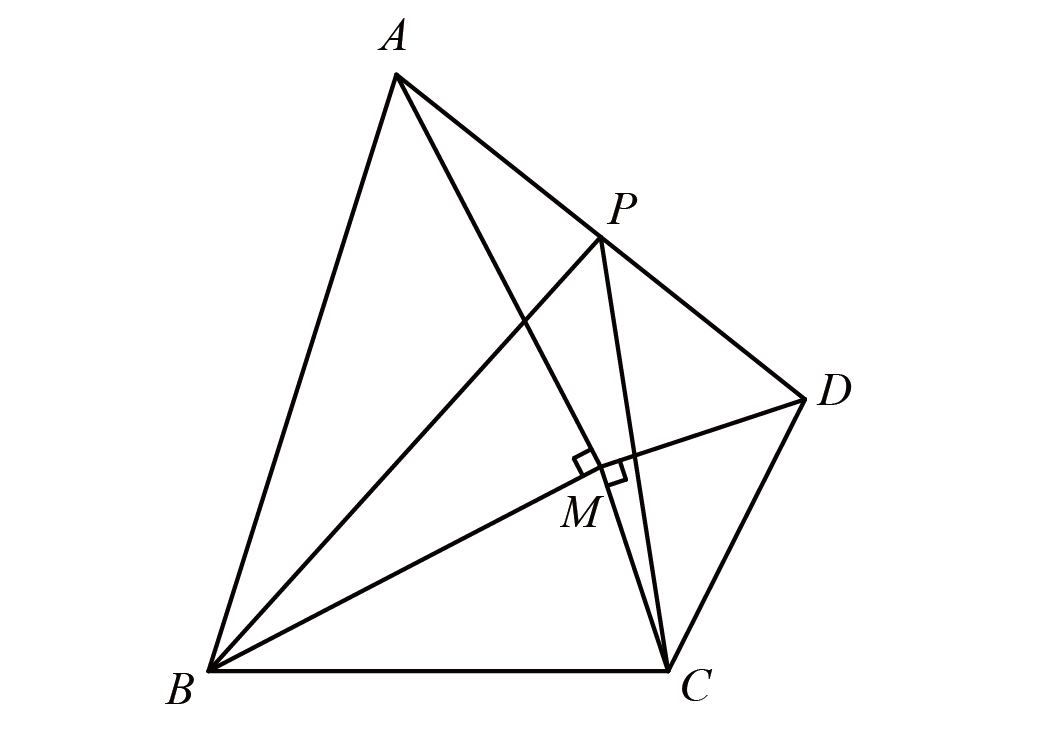
当一条直线交$\triangle ABC$三边所在的直线分别于点$X$、$Y$、$Z$时，则有$\dfrac{AX}{XB}\times \dfrac{BZ}{ZC}\times \dfrac{CY}{YA}=1$．

梅涅劳斯（Menelaus）定理（简称梅氏定理）最早出现在由古希腊数学家梅涅劳斯的著作《球面学》（Sphaerica）中，此题运用的是四边形的梅涅劳斯定理，当然小学也可以使用燕尾模型来做．