【小奥】问题10 整数点有几个？

问题

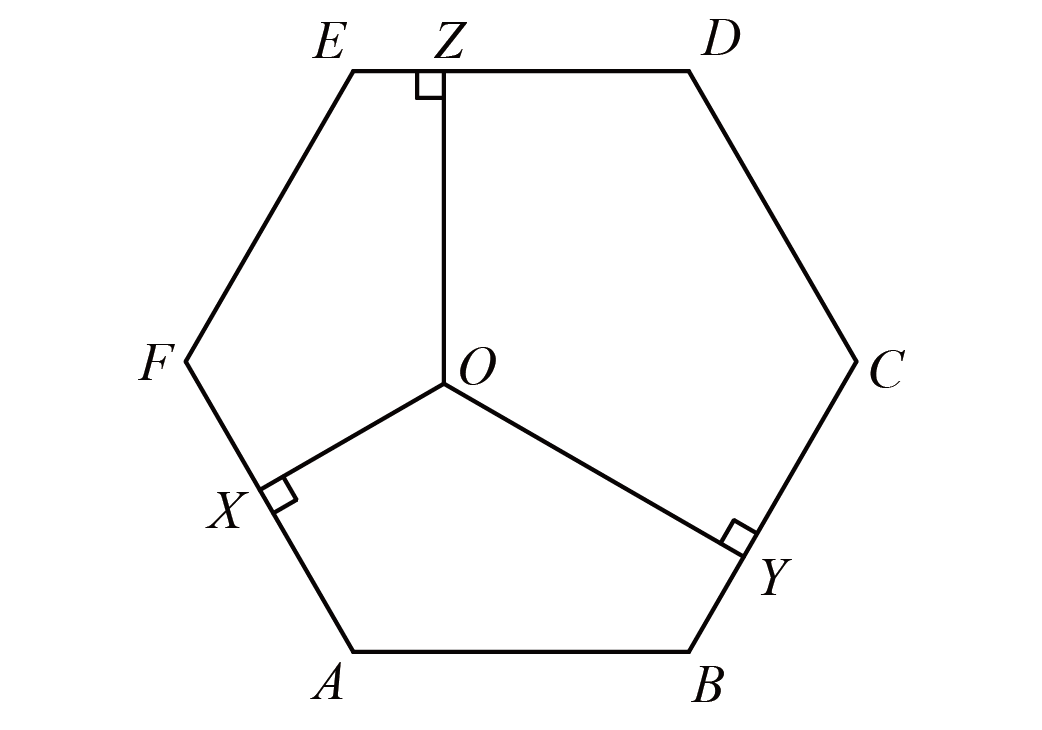
如图，正六边形$ABCDEF$相对两边之间的距离为$6$，点$O$为正六边形内部一点，过$O$分别向三条线段$AF$、$BC$、$DE$作垂线，交点分别为$X$、$Y$、$Z$（$X$、$Y$、$Z$分别在线段$AF$、$BC$、$DE$上），那么使得$OX$、$OY$、$OZ$都是整数的点$O$一共有多少个？

法1

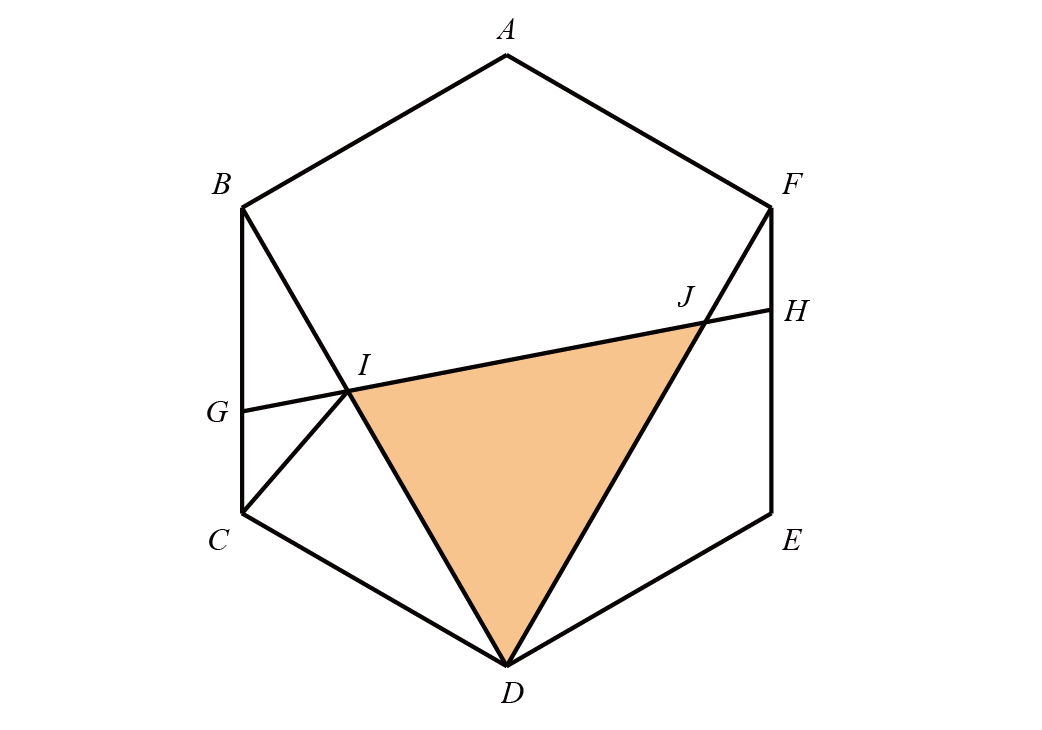
如图，将正六边形各边延长变成正三角形$GHI$，过$I$作$IJ$垂直$GH$于$J$，则
$$OX+OY+OZ=IJ=6\times \dfrac{3}{2}=9$$

因为$O$为正六边形内部一点，$OX$、$OY$、$OZ$不为$0$，若三条线段至少为$2$，这样的$O$一共有$C_{5}^{2}=10$个

若三条线段中有$1$，则只能是$1$、$4$、$4$，这样的情况有$3$种，共$10+3=13$个．

法2

如图，将正六边形等分，因此这样的点一共有$13$个