2024华师一附中丘班游园考试真题

整体难度不大，但是题量较大，分为2个部分，第一部分初阶数学思维，60分钟一共20道填空，每题4分，两道解答每题10分，共100分，第二部分为高阶数学思维，30分钟，5道单空题，5道双空题，每题5分，共50分，两个部分总计150分

以下题目全部来自我的学生回忆版整理而来，不保证准确性，部分题目的表达没有校对，答案暂未更新，后续再更新。

如果有新题目欢迎补充

1. 解方程：$[x]=3x-2$，$x=\underline{\qquad}$。
2. $15$化成$2$进制是$\underline{\qquad}$，$10$位的$2$进制数有$\underline{\qquad}$个。
3. $\varphi(x)$表示不超过$x$的非$0$自然数中与$x$互质的自然数的个数，$\varphi(25)=\underline{\qquad}$，$\varphi(77)=\underline{\qquad}$。
4. 甲乙丙$3$人从$A$地出发去$270\text{km}$远的$B$地，每天走$10\text{km}$，每人最多带$36$天的食物，可以把食物分给他人。
   $(1)$若甲乙两人出发，甲距离$A$地$100\text{km}$时返回，乙可以走$\underline{\qquad}$千米就要返回;
   $(2)$若甲乙两人出发，乙最多可以走$\underline{\qquad}$千米就要返回;
   $(3)$请设计一种方案，可以互相补给，不可以存放，如何让乙走到$B$再返回。
5. 一批衣服进价$40$元，打算以$40\%$的利润卖出，卖了$80\%$后打折，卖完后的总利润只有原来的$86\%$，则打了$\underline{\qquad}$折。
6. 对于一些数$a_{1}$，$a_{2}$，$\cdots$，$a_{n}$，若$a_{i}>a_{j}$且$i<j$，则成$a_{i}$，$a_{j}$为逆序，$a_1$到$a_n$的逆序数量叫逆序数
   $(1)1$，$2$，$3$，$4$的任意排列中，逆序数恰好为$2$的排列有$\underline{\qquad}$个;
   $(2)$设$a_1$，$a_2$，$\cdots$，$a_{10}$的逆序数为$k$，则$a_{10}$，$a_{9}$，$\cdots$，$a_1$的逆序数为$\underline{\qquad}($用$k$表示$)$。
7. 计算：$1+\dfrac{1}{1+2}+\dfrac{1}{1+2+3}+\cdots+\dfrac{1}{1+2+3+\cdots+2024}=\underline{\qquad}$。
8. 小明一步跨$2$级或$3$级台阶，一共$20$级台阶有$\underline{\qquad}$种不同的走法。
9. 有一堆石子，甲乙两人轮流取，甲先取，乙后取，每次$1-5$颗，如果一共$12$颗，$\underline{\qquad}$必胜，$2024$颗$\underline{\qquad}$必胜。
10. 有一个水池，单开甲管$12$个小时可以注满，单开乙管$20$个小时可以注满，现在甲开$1$个小时，乙开$1$个小时，轮流下去，注满水池要$\underline{\qquad}$小时。
11. 把圆柱体切成$2$个小的圆柱体，它的表面积增加了$25.12$平方分米，把它切成两个半圆柱体，它的表面积增加$80$平方分米，这个圆柱体的体积时$\underline{\qquad}$立方分米。
12. 给一块长方形区域铺地砖，这个长方形的长是$2050$厘米，宽是$615$厘米。要往里面铺入最大的正方形地砖，且没有剩余，这样的正方形地砖有$\underline{\qquad}$块。
13. 如果一组数对于一种运算满足以下三个性质，就说这组数对于这个运算是优美的，性质一：进行这个运算后得到的结果还在这组数内，性质二：一定存在一个数$e$，使得数$x$与$e$进行运算结果为数$x$本身，性质三：对于任意$x$，一定存在另一个数$y$使得$x$与$y$运算得到的结果等于$y$与$x$运算，且这个结果为$e$，以下四组数和运算中，$\underline{\qquad}$满足这组数对于这个运算是优美的。
    A.自然数和加法
    B.自然数和乘法
    C.整数和加法
    D.整数和乘法
14. 数学家祖冲之曾给出圆周率$\pi$的两个近似值：”约率”$\dfrac{22}{7}$与”密率”$\dfrac{355}{113}$。他们可用”调日法”得到：称大于$\pi$的近似值为强率，小于$\pi$的近似值为弱率，由$\dfrac{3}{1}<\pi<\dfrac{4}{1}$，取$3$为初始弱率，$4$为初始强率，得$a_1=\dfrac{3+4}{1+1}=\dfrac{7}{2}$，故$a_1$为强率，与上一次的弱率$3$计算得$a_2=\dfrac{3+7}{1+2}=\dfrac{10}{3}$，故$a_2$为强率，继续计算，$\cdots\cdots$，若某次得到的近似率为强率，与上一次得弱率计算得到新的近似值，若某次得到的近似值为弱率，与上一次得强率继续计算得到新的近似值，以此类推，已知$a_m=\dfrac{22}{7}$，则$m=\underline{\qquad}$，$a_7=\underline{\qquad}$。
15. 若一个三角形的任意两边都不相等，则称之为不规则三角形$,$用一个正方体上的任意三个顶点构成的所有三角形中，不规则三角形的个数是$\underline{\qquad}$。
16. 一串数：$1,2,4,8$……从第二个开始$,$每一个都是前一个的两倍。$X_n$表示数串中小于等于$n$的个数，$X_1+X_2+$……$+X_{49}+X_{50}=\underline{\qquad}$。
17. 一个立方体框架，用一支手电筒照上去，影子可能是$\underline{\qquad}$种样子。

18. 如图，四边形$ABCD$的面积为$6$，将$BA$、$AD$、$DC$、$CB$延长$3$倍得到新的四边形$EFGH$，四边形$EFGH$的面积是$\underline{\qquad}$。
    

19. 如图，三个正方形摆放如下，阴影部分的面积是$\underline{\qquad}$。
    

20. 设“一家之言”、“言扬行举”、“举世皆知”、“知行合一”四个成语中的每个汉字代表$11$个连续的非零自相同的汉字代表相同的数，不同的然数中的一个，汉字代表不同的数，如果每个成语中四个汉字所代表的数之和都是$21$，则“行”可以代表的数最大是$\underline{\qquad}$。

21. “数缺形不直观，形缺数不入微”，数形结合思想是数学学习中的一个重要的数学思想，请仔细观察下面几幅图形并回答后面的问题：
    
    ①由图形$\underline{\qquad}$可知勾股定理$a^2+b^2=c^2$成立；
    ②由图形$\underline{\qquad}$可知完全平方公式$(a+b)^2=a^2+b^2=2ab$成立
    ③由图形$\underline{\qquad}$可知平方差公式$a^2-b^2=(a+b)(a-b)$成立
    ④由图形$\underline{\qquad}$可知公式$(a+b)^2-(b-a)^2=4ab$成立

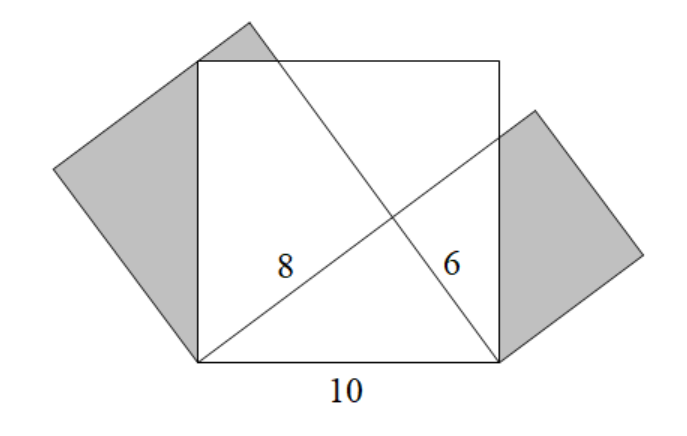
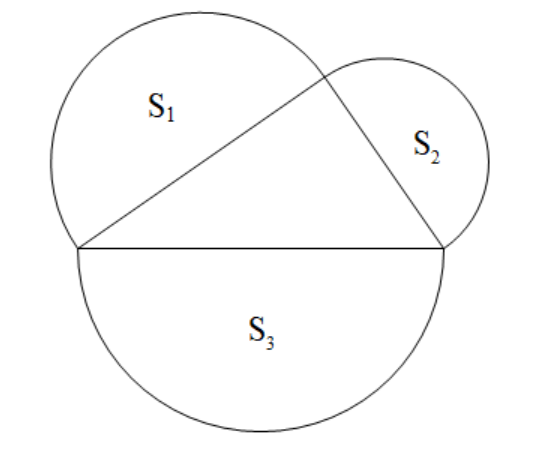
22. 如图是一个直角三角形，以三条边为直径作三个半圆，面积分别是$S_1$、$S_2$、$S_3$，它们之间的关系是$\underline{\qquad}$。