【小奥】问题56 三个正方形求面积

问题

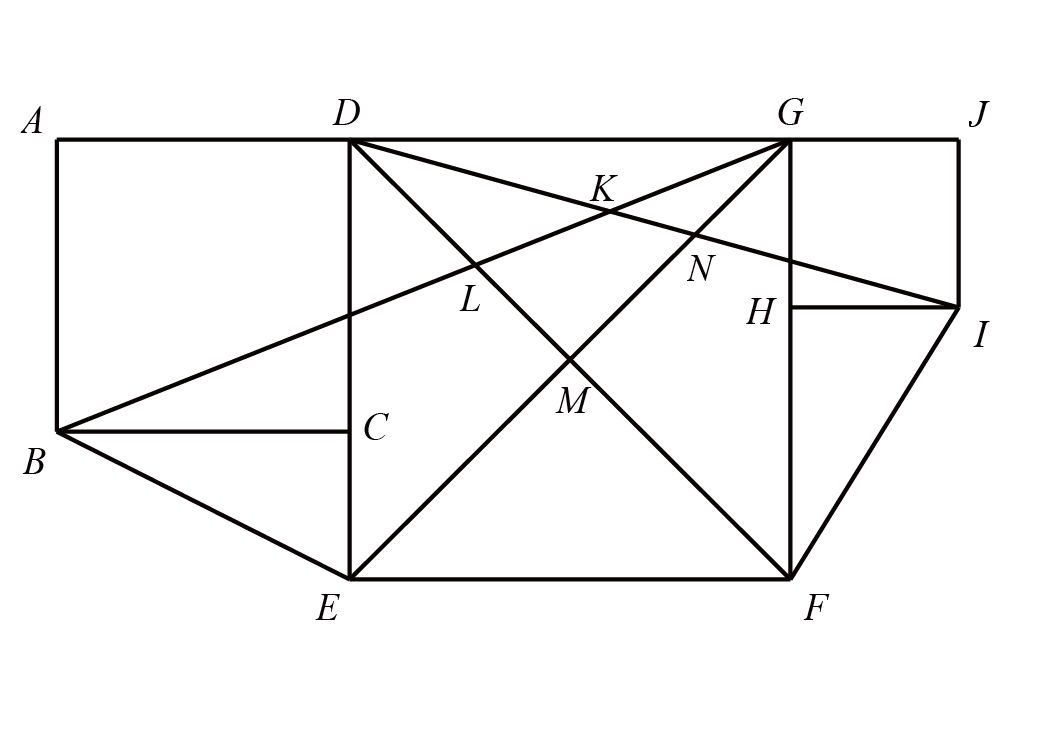
如图，四边形$ABCD$、$DEFG$、$GHIJ$都是正方形，$BG$、$EG$、$DF$、$DI$分别交于点$K$、$L$、$M$、$N$，已知$S_{\triangle DLK}=25$，$S_{BEML}=81$，$S_{MNKL}=36$，$S_{MFIN}=75$。
$(1)$三角形$GKN$的面积是多少？
$(2)$正方形$DEFG$的面积是多少？

解析

如图，连接$BD$、$GI$，因为$BD$//$EG$，$GI$//$DF$

所以$$S_{\triangle BEG}=S_{\triangle DEG}$$

$$S_{\triangle DFI}=S_{\triangle DFG}$$

又因为$$S_{\triangle DEG}=S_{\triangle DFG}$$

所以$$S_{\triangle BEG}=S_{\triangle DFI}$$

那么$$S_{\triangle GKN}=25+75-81=19$$

$$S_{DEFG}=2S_{\triangle DFI}=2\times(25+36+75)=272$$