【小奥】问题57 六条线段相等求角度

问题

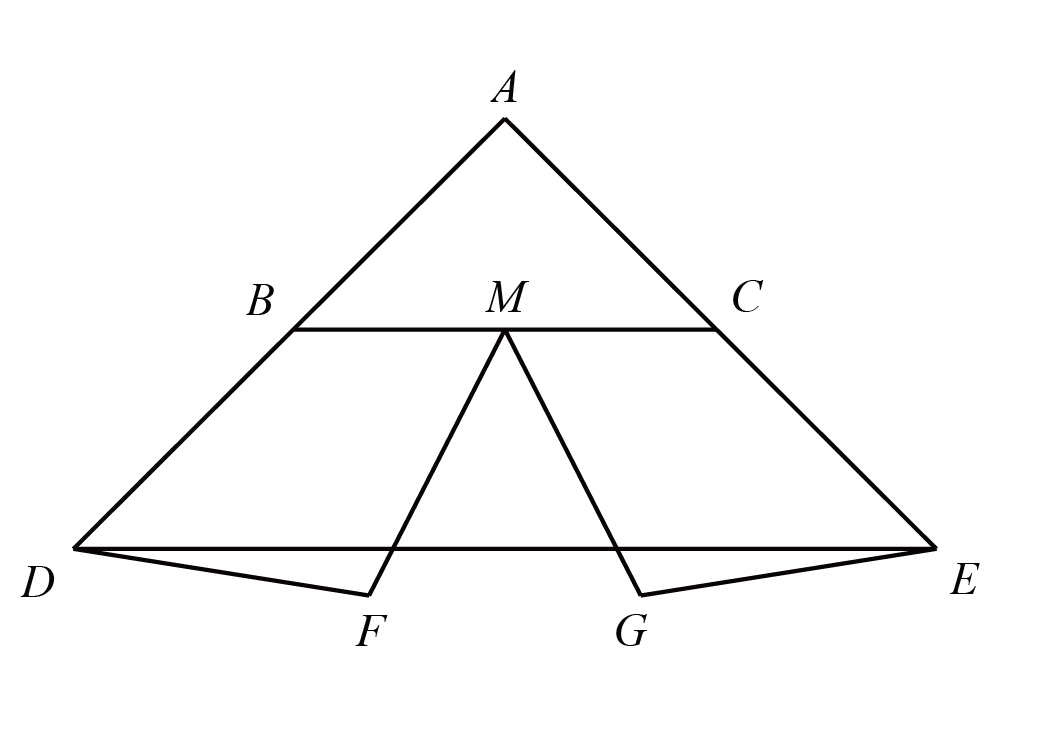
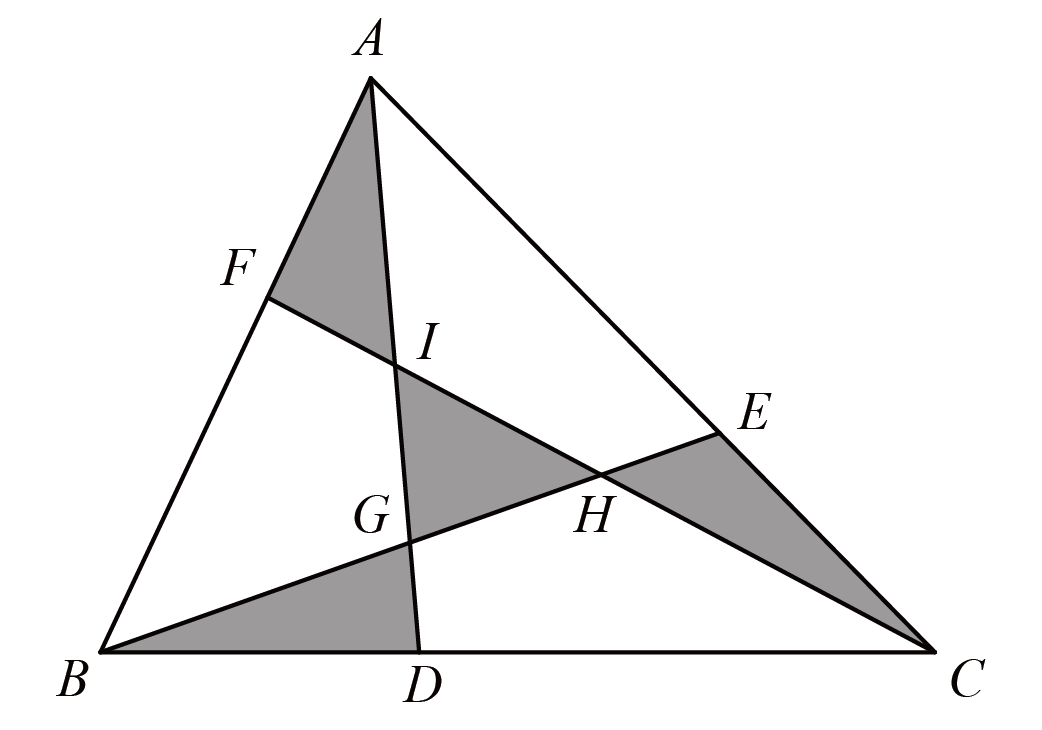
如图，$\triangle ABC$和$\triangle ADE$都是等腰直角三角形，$\angle BAC=90^{\circ}$，$M$是$BC$的中点，且$AB=AC=DF=FM=GM=GE$，$\angle FDE=\angle GED=9^{\circ}$，求$\angle FMG$。

解析

如图，构造正方形$APBM$，作$F$关于$AD$的对称点$Q$，连接$DQ$、$PQ$、$PM$

易得$$PM=AB=MF=FD=DQ=QP$$

并且$$\angle QDF=2\angle ADF=2\times (45^{\circ}+9^{\circ})=108^{\circ}$$

所以$PQDFM$是正五边形，右边同理，因此

$$\angle FMG=360^{\circ}-108^{\circ}\times 2-90^{\circ}=54^{\circ}$$