【小奥】问题25 直角三角形求面积

问题

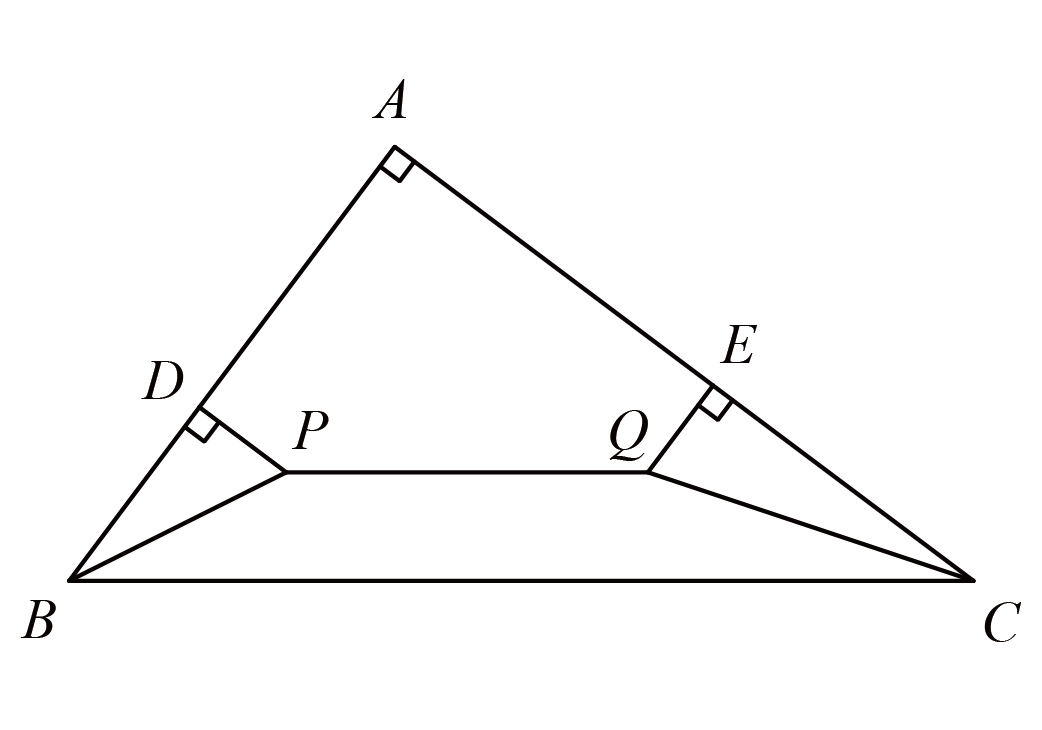
如图，直角三角形$ABC$中，$\angle A=90^{\circ}$，$AB=18cm$，$AC=24cm$，$BC=30cm$．$\angle ABP=CBP$，$\angle ACQ=\angle BCQ$，$PQ$和$BC$平行．过$P$作$AB$边上的垂线$PD$，过$Q$作$AC$边上的垂线$QE$．$PD=2.4cm$．

（1）五边形$ADPQE$的面积是多少？

（2）$PQ$的长度是多少？

解析

（1）如图，三角形$BDP$和三角形$BFP$面积相等，三角形三角形$QCE$和三角形$QCG$面积相等，长方形$BCGF$的面积为$30\times 2.4 =72$，所以五边形$ADPQE$的面积为$18\times 24 \div 2 -72=144$．

（2）如图，将三角形$QCE$平移至三角形$PFH$，过$P$作$PG$和$BF$垂直，延长$FH$交$AB$于$I$，则$PD=PG=PH=2.4$，且

$$BI:IF:BF=18:24:30=3:4:5$$

设$BI=3x$，则$IF=4x$，$BF=5x$，根据面积法易得

$$(3x+4x+5x)\times 2.4 \div 2=3x\times 4x \div 2$$

解得$x=2.4$，所以$BF=2.4\times 5=12$，所以

$$PQ=FC=30-12=18$$