题目

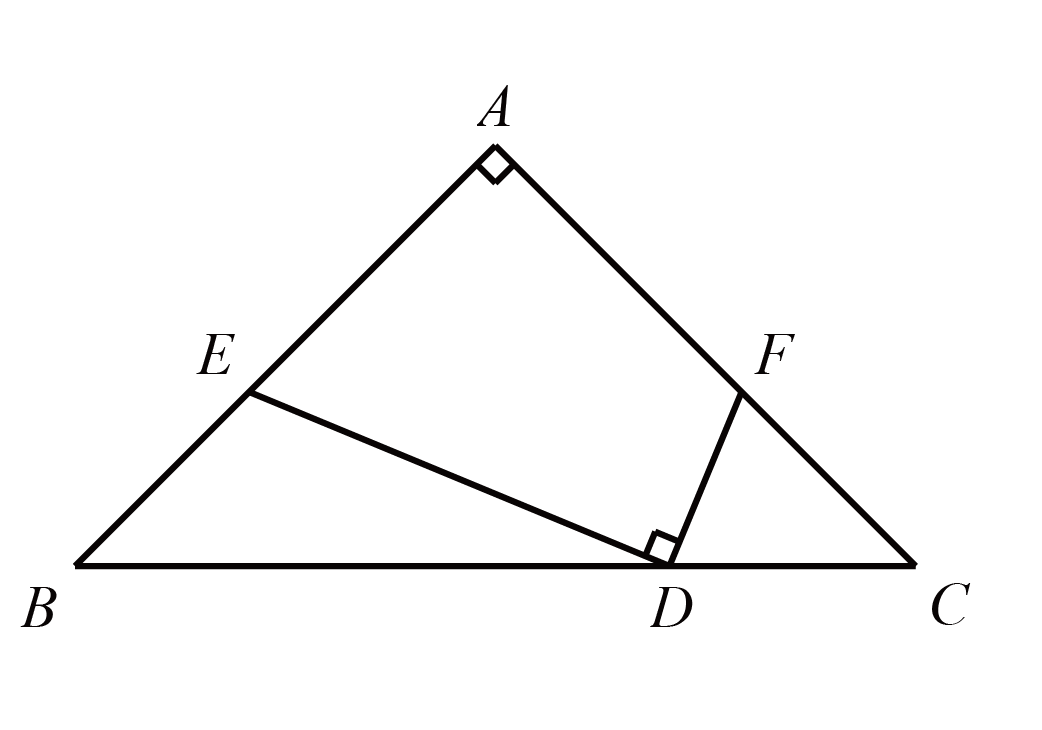
如图，等腰直角$\triangle ABC$中，$AB=AC$，$\angle A=90^{\circ}$，$D$为$BC$上一点，$E$为$AB$上一点，$F$为$AC$上一点，且$AE=AF$，$\angle EDF=90^{\circ}$，$\angle BDE=22.5^{\circ}$，$DE=9\mathrm{cm}$
$(1)$求四边形$AEDF$的面积。
$(2)$求$\triangle EBD$的面积。

解答

(1)$\because AE=AF$、$\angle BAD= \angle EDF= 90^{\circ}$
$\therefore \triangle ADF$绕点$A$顺时针旋转$90^{\circ}$到$\triangle AWE$
$\therefore W$、$E$、$D$共线，$\triangle AWD$是等腰$\text{Rt} \triangle$
$\therefore \angle ADE=45 ^{\circ}$
$\because AED=45 ^{\circ} + 22.5 ^{\circ} =67.5 ^{\circ}$
$\therefore AW=AD=DE=9$
$\therefore S_{AEDF } = S_{\triangle AWD } = \dfrac{ 1 }{ 2 } \times 9 \times 9=40.5 \text{cm}^2$

(2)如图，过点$E$作$EX \perp AB$交$BC$于$X$，则$\triangle BEX$是等腰直角三角形，构造弦图，则$BZ=EY$
$\because \angle BXE=45 ^{\circ}$，$\angle EDB = 22.5 ^{\circ}$
$\therefore XE=XD$
$\therefore BZ=EY=YD= \dfrac{ 1 }{ 2 } DE=4.5$
$\therefore S_{\triangle BED } = \dfrac{ 1 }{ 2 } \times 9 \times 4.5 = 20.25 \text{cm}^2$