北京朝阳2023端午思维龙舟会，朝阳期末考试后，五年级部分同学参加的活动。PDF下载

2023 年 “端午节” 思维龙舟会

时间： $1: 30-3: 00$
娃名$\underline{\hspace{3em}}$ 学校$\underline{\hspace{3em}}$ 年级$\underline{\hspace{3em}}$ 得分$\underline{\hspace{3em}}$
以下题目每题 5 分一共 100 分

屈原是我国著名的古代诗人，他生活在春秋战国时期的$\underline{\hspace{3em}}$。他的代表作品有《离骚》、《天问》和《九歌》等。屈原忠诚于国家，但在政治上受到排挤，最终投汨罗江自尽。
为了纪念屈原，每年农历五月初五，人们会庆拀一个节日，这个节日叫做$\underline{\hspace{3em}}$节。
算式 $1+2+3+\ldots+10=\underline{\hspace{3em}}$。
屈原在楚国朝廷中担任大夫的年数是$ 25 $年，如果他在楚国朝廷中任职共$ 30 $年，那么他还担任了其他职位$\underline{\hspace{3em}}$年。
假设屈原的《离骚》用了$ 2984 $个汉字，一共$ 373 $行，那么平均每行有$\underline{\hspace{3em}}$个汉字。
端午节是为了纪念屈原，每年端午节，村子里有$ 8 $艘龙舟参加龙舟比赛。如果每膄龙舟上有$20$名划船队员，那么共有$\underline{\hspace{3em}}$名队员参加比赛?
某城市为纪念屈原，决定举办端午节登山活动。参与登山活动的人数为$ 202 $人。这$ 202 $人需要分成$ 41 $个小组，每个小组的人数不一定相同。已知每个小组的人数必须是一个质数。那么人数最少的小组有$\underline{\hspace{3em}}$人。
端午节当天，一家公司决定举办一场数学竞赛来纪念屈原。比赛中有一个涉及数字拆分的问题。请将$2023 $拆分为两个正整数的和，使得这两个数的乘积最大。那么这个最大的乘积等于$\underline{\hspace{3em}}$。
在端午节庆祝活动中，有 $4$ 个地方发放棕子。已知 $\mathrm{A}$ 地发放了 $20$ 个粽子，$\mathrm{B}$ 地发放了$ 30 $个粽子，$\mathrm{C}$ 地发放了$ 40 $个棕子，那么$\mathrm{D}$ 地至少需要发放$\underline{\hspace{3em}}$粽子才能使四个地方总共发放的棕子数达到 $100 $个?
算式$\dfrac{4 \times 5 \times 6+8 \times 9 \times 10+12 \times 13 \times 14+\cdots+200 \times 201 \times 202}{\left(2^{2} \times 3+3^{2} \times 2\right)+\left(4^{2} \times 5+5^{2} \times 4\right)+\left(6^{2} \times 7+7^{2} \times 6\right)+\cdots+\left(100^{2} \times 101+101^{2} \times 100\right)}$
的计算结果是$\underline{\hspace{3em}}$。
$\overline{a b c d}$ 能被$ 11 $整除，被$ 5 $除余$ 3$ ，并且 $a+b+c=15$，$b+c+d=19$，则 $\overline{a b c d}=\underline{\hspace{3em}}$。
在端午节龙舟赛上，一根长$2023$厘米的木棍被用作装饰。从左到右，每隔$7$厘米染上一个红点，同时从右到左，每隔$6$厘米染上一个红点。如果在比赛结束后，沿着红点将木棍锯开，那么一共锯成$\underline{\hspace{3em}}$段。
在纪念屈原的端午节龙舟赛活动中，组织者准备了一个封闭的正方体纸盒装礼物，纸盒由$ 6 $个正方形面组成。为了迅速将礼物分发给参赛者，组织者希望将纸盒沿着最少的棱剪开，便其平铺成一个相连的$6$个正方形组成的平面图形。那么组织者需要前开纸盒的最少棱数是$\underline{\hspace{3em}}$。
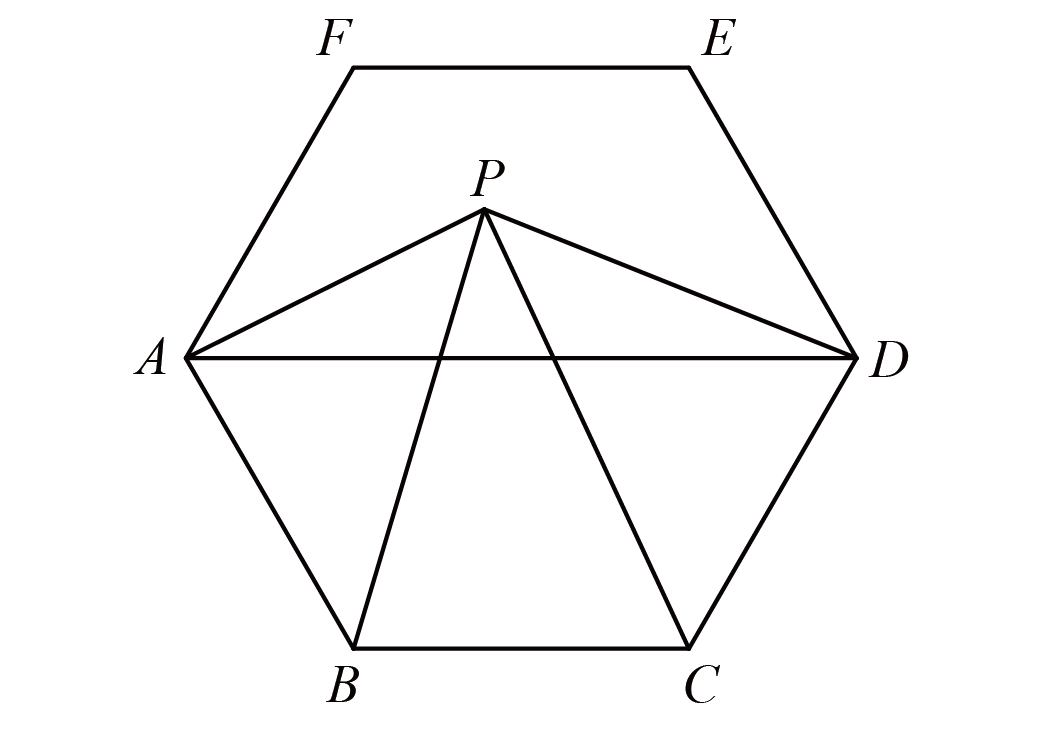
如右图，三角形 $A B C$ 中，$A F: F B=B D: D C=C E: A E=5: 3$，且三角形 $G H I$ 的面积是 8，那么三角形 $A B C$ 的面积是$\underline{\hspace{3em}}$。
纪念屈原的端午节龙舟赛中，组织者为了让比赛更具趣味性，设置了一个有关连续奇数的问题，从$1 $开始的连续奇数：$1$、$3$、$5$、$7$、……、$2021$、$2023$，这些数的数字之和是$\underline{\hspace{3em}}$。
在纪念屈原的端午节龙舟赛中，共有$ 200 $名运动员参加。他们的编号分别为$ 1 $到$ 200$。组织者为了让参赛者更了解数学知识，要求每位运动员在黑板上写下自己编号中的最大奇因子。那么运动员在黑板上写下所有数之和是$\underline{\hspace{3em}}$。
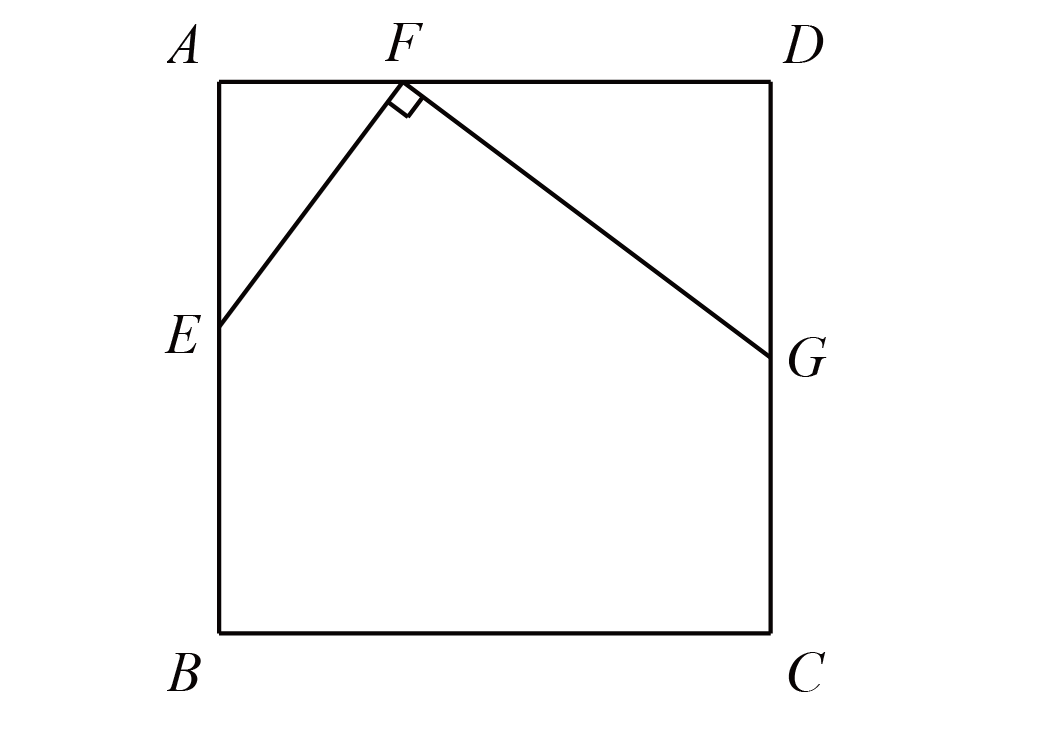
如图，一块面积为$ 50 $的正方形地砖，上面印有四周对称的花纹，其上的两个同心圆，恰好分别经过等腰直角三角形的顶点，若四块等腰直角三角形的总面积是$ 18 $，那么大、小圆的面积的比值为$\underline{\hspace{3em}}$。
现有甲、乙、丙、丁四个工程队，甲、乙、丙各接受一个工作量相同的工程. 这四个队单独完成这个工程所用时间依次分别是 $28 、 24 、 20 、 30$ 天. 甲、乙、丙三个队同时开工，丁队先帮甲队工作 $x$ 天，接着帮乙队工作 $y$ 天，最后帮助丙队工作 $z$ 天一直到完工. 如果 $x 、 y$ 是整数且甲、乙、丙三队在同一天内完工，则 $x 、 y 、 z$ 的乘积为$\underline{\hspace{3em}}$。
在纪念屈原的端午节龙舟赛中，组织者设置了一个有趣的数学问题。如果把一个数与这个数的数字和之比的比值称为 “平均位值”，那么所有三位数的 “平均位值”之和是$\underline{\hspace{3em}}$。
在纪念屈原的端午节龙舟赛中，甲、乙两名运动员参加了一项特殊的陆地竞速比赛。他们从一条直线跑道的起点出发，速度分别是每分钟$ 40 $米和$ 50 $米。甲的速度每过一分钟增加$ 1 $米每分，乙的速度每过一分钟都增加或者减少$ 2 $米每分。在这场比赛中，经过$ 60 $分钟，两个人最多相互追及$\underline{\hspace{3em}}$次。