七年级含参不等式整数解最值问题

问题

已知$\dfrac{7}{13}$<$\dfrac{n}{n+k}$<$\dfrac{6}{11}$，其中$n$、$k$为正整数。
（$1$）对于某一个$n$，若只有$1$个$k$使不等式$\dfrac{7}{13}$<$\dfrac{n}{n+k}$<$\dfrac{6}{11}$成立，则$n$的最小值和最大值分别是多少？
（$2$）对于某一个$n$，若只有$3$个$k$使不等式$\dfrac{7}{13}$<$\dfrac{n}{n+k}$<$\dfrac{6}{11}$成立，则$n$的最小值和最大值分别是多少？

解析

先考虑最大

$\because \dfrac{7}{13}<\dfrac{n}{n+k}<\dfrac{6}{11} $

$\therefore \dfrac{13}{7}>\dfrac{n+k}{n}>\dfrac{11}{6} $

$\therefore\dfrac{6}{7}>\dfrac{k}{n}>\dfrac{5}{6}$

$\therefore \dfrac{5}{6} n<k<\dfrac{6}{7} n $

若只有$1$个$k$成立，则 $\dfrac{6}{7} n-\dfrac{5}{6} n \leqslant 2 \Rightarrow \dfrac{1}{42} n \leqslant 2 \Rightarrow n \leqslant 84$

若只有$3$个$k$成立，则 $\dfrac{6}{7} n-\dfrac{5}{6} n \leqslant 4 \Rightarrow \dfrac{1}{42} n \leqslant 4 \Rightarrow n \leqslant 168$

再考虑最小

$\because\dfrac{6}{7}>\dfrac{k}{n}>\dfrac{5}{6}$

$\therefore \begin{cases}6n>7k \\ 6k>5n\end{cases}$

$\therefore \begin{cases}6 n-1 \geqslant 7 k \\ 6 k \geqslant 5 n+1\end{cases}$

$\therefore \dfrac{6 n-1}{7} \geqslant k \geqslant \dfrac{5 n+1}{6}$

若只有$1$个$k$成立，则$\dfrac{6 n-1}{7}-\dfrac{5 n+1}{6} \geqslant 0 \Rightarrow n \geqslant 13$

若只有$3$个$k$成立，则$\dfrac{6 n-1}{7}-\dfrac{5 n+1}{6} \geqslant 2 \Rightarrow n \geqslant 97$

经验证都成立

代码验证

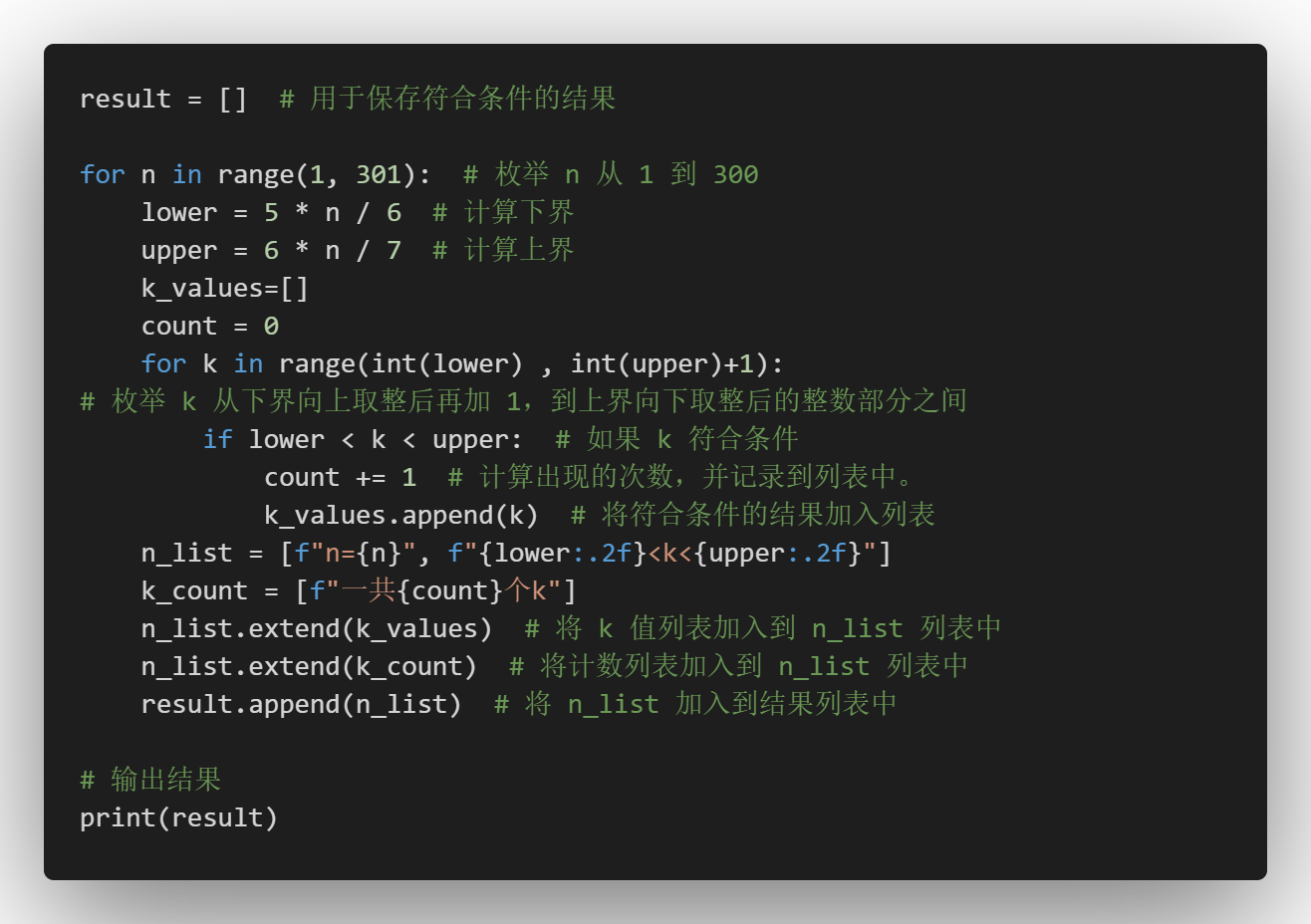
result = []  # 用于保存符合条件的结果

for n in range(1, 301):  # 枚举 n 从 1 到 300
    lower = 5 * n / 6  # 计算下界
    upper = 6 * n / 7  # 计算上界
    k_values=[]
    count = 0
    for k in range(int(lower) , int(upper)+1):  # 枚举 k 从下界向上取整后再加 1，到上界向下取整后的整数部分之间
        if lower < k < upper:  # 如果 k 符合条件
            count += 1  # 计算出现的次数，并记录到列表中。
            k_values.append(k)  # 将符合条件的结果加入列表
    n_list = [f"n={n}", f"{lower:.2f}<k<{upper:.2f}"]
    k_count = [f"一共{count}个k"]
    n_list.extend(k_values)  # 将 k 值列表加入到 n_list 列表中
    n_list.extend(k_count)  # 将计数列表加入到 n_list 列表中
    result.append(n_list)  # 将 n_list 加入到结果列表中

# 输出结果
print(result)

['n=1', '0.83<k<0.86', '一共0个k'], 
['n=2', '1.67<k<1.71', '一共0个k'], 
['n=3', '2.50<k<2.57', '一共0个k'], 
['n=13', '10.83<k<11.14', 11, '一共1个k'], 
['n=14', '11.67<k<12.00', '一共0个k'], 
['n=84', '70.00<k<72.00', 71, '一共1个k'], 
['n=85', '70.83<k<72.86', 71, 72, '一共2个k'], 
['n=86', '71.67<k<73.71', 72, 73, '一共2个k'], 
['n=87', '72.50<k<74.57', 73, 74, '一共2个k'], 
['n=96', '80.00<k<82.29', 81, 82, '一共2个k'], 
['n=97', '80.83<k<83.14', 81, 82, 83, '一共3个k'], 
['n=98', '81.67<k<84.00', 82, 83, '一共2个k'], 
['n=99', '82.50<k<84.86', 83, 84, '一共2个k'], 
['n=168', '140.00<k<144.00', 141, 142, 143, '一共3个k'], 
['n=169', '140.83<k<144.86', 141, 142, 143, 144, '一共4个k'], 
['n=170', '141.67<k<145.71', 142, 143, 144, 145, '一共4个k'], 
['n=171', '142.50<k<146.57', 143, 144, 145, 146, '一共4个k'], 
['n=172', '143.33<k<147.43', 144, 145, 146, 147, '一共4个k'],