【小奥】问题30 阴影面积相等求边长比

问题

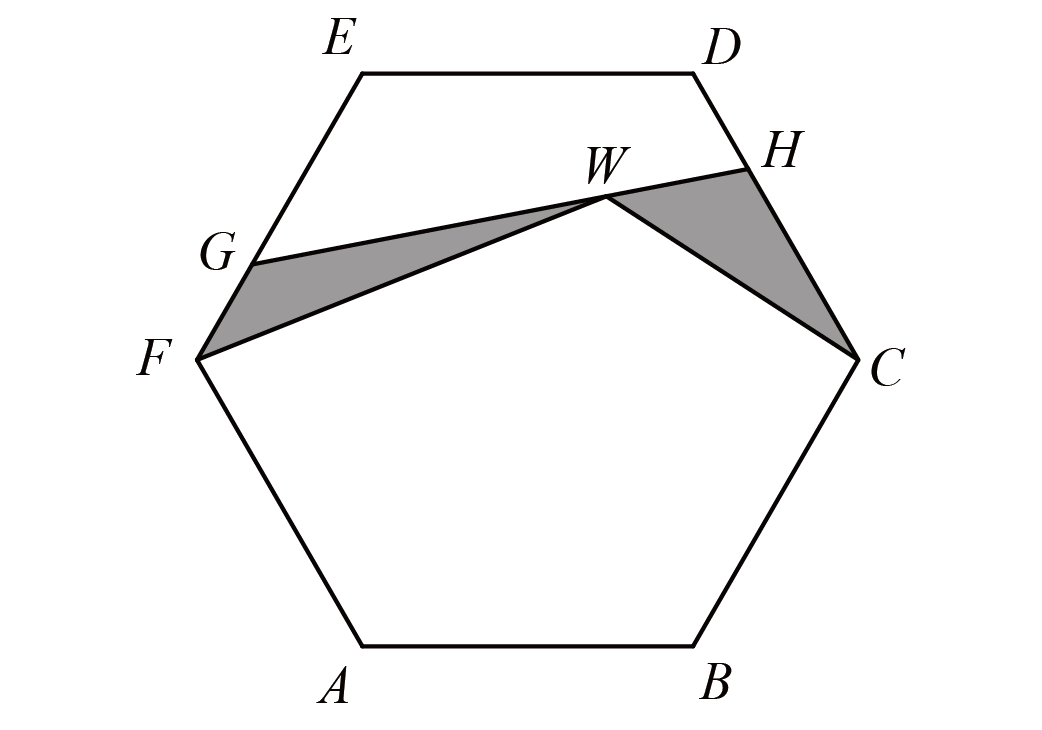
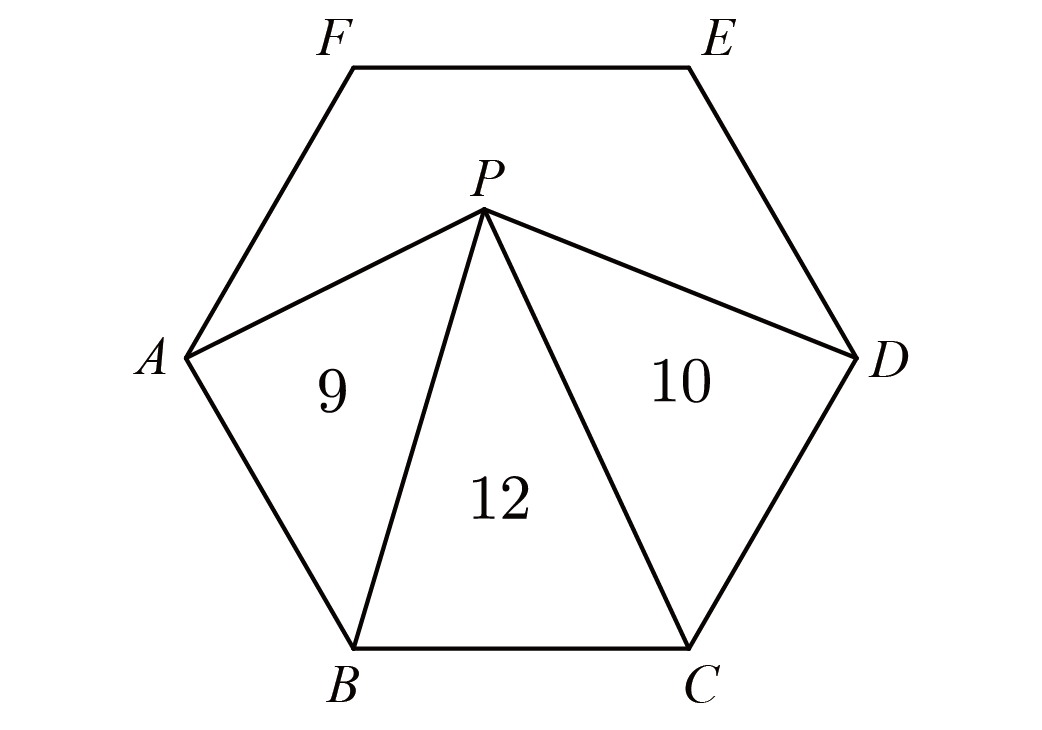
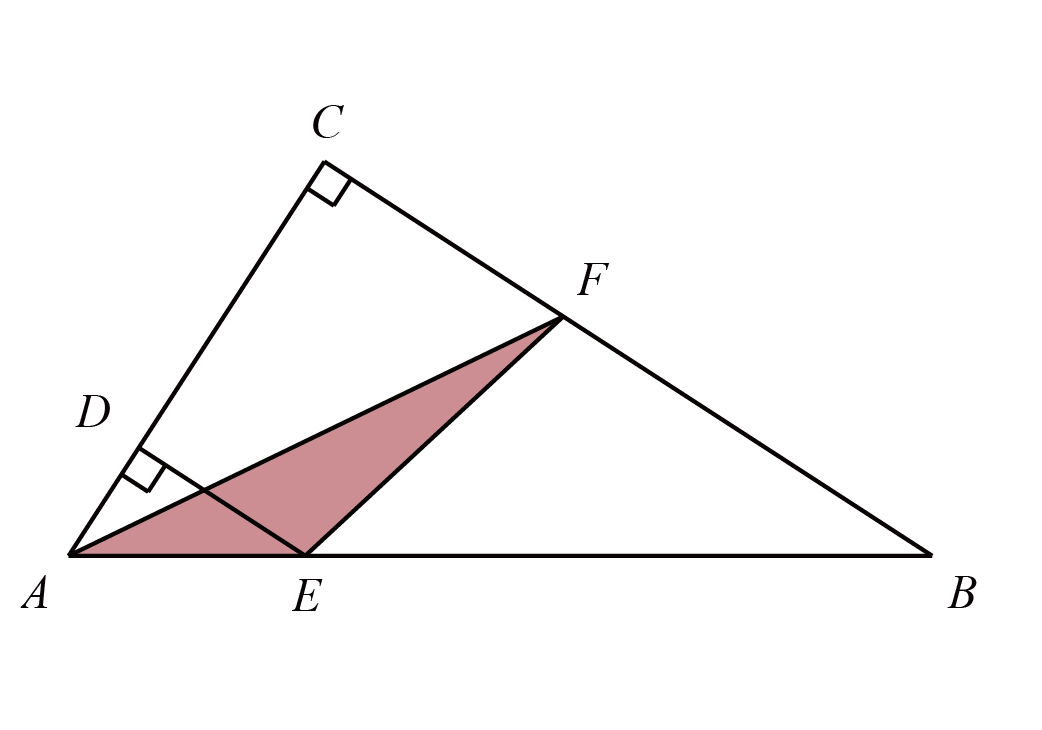
如图，正六边形$ABCDEF$中，$EG=2GF$，$HC=2DH$，连接$GH$，$W$是$GH$上的一点，已知图中两块阴影部分的面积相等，求$GW:WH$．

法1

如图，连接$CF$，$WE$，$WD$，延长$FE$和$CD$交于点$I$，连接$WI$，则$EF=EI$，$DI=DC$

设两块阴影部分的面积为$2a$，则$S_{\triangle EGW}=4a$，$S_{\triangle EIW}=6a$，$S_{\triangle DHW}=a$，$S_{\triangle DIW}=3a$

所以$GW:WH=S_{\triangle GWI}:S_{\triangle HWI}=10a:4a=5:2$．

法2：【上海】石头

如图，连接$CG$，$FH$，延长$FE$和$CD$交于点$I$，易得$IG:GF=5:1$，$IH:HC=4:2=2:1$，设$S_{\triangle GHI}=10$，则
$$S_{\triangle GFH}=10\times \dfrac{1}{5}=2$$

$$S_{\triangle GHC}=10\times \dfrac{1}{2}=5$$

又
$$S_{\triangle GFH}=S_{\triangle GFW}\times \dfrac{GH}{GW}$$

$$S_{\triangle GHC}=S_{\triangle WHC}\times \dfrac{GH}{WH}$$

因为$S_{\triangle GFW}=S_{\triangle WHC}$，所以
$$GW:WH=S_{\triangle GHC}:S_{\triangle GFH}=5:2$$

法3：【北京】酒吞

如图，连接$FC$、$OG$、$OW$、$OH$，根据毕克定理易得
$$S_{\triangle OFG}=2\times (0+5\div 2-1)=3$$

$$S_{\triangle OGH}=2\times (3+3\div 2-1)=7$$

$$S_{\triangle OHC}=2\times (1+6\div 2-1)=6$$

因为$S_{\triangle OWF}=S_{\triangle OWC}$，所以

$$S_{OWGF}=S_{OWHC}=(3+7+6)\div 2=8$$

因此$S_{\triangle OGW}=8-3=5$，$S_{\triangle OHW}=8-6=2$，所以

$$GW:WH=S_{\triangle OGW}:S_{\triangle OHW}=5:2$$