【小奥】问题51 已知两块阴影部分的大小求正六边形的面积

问题

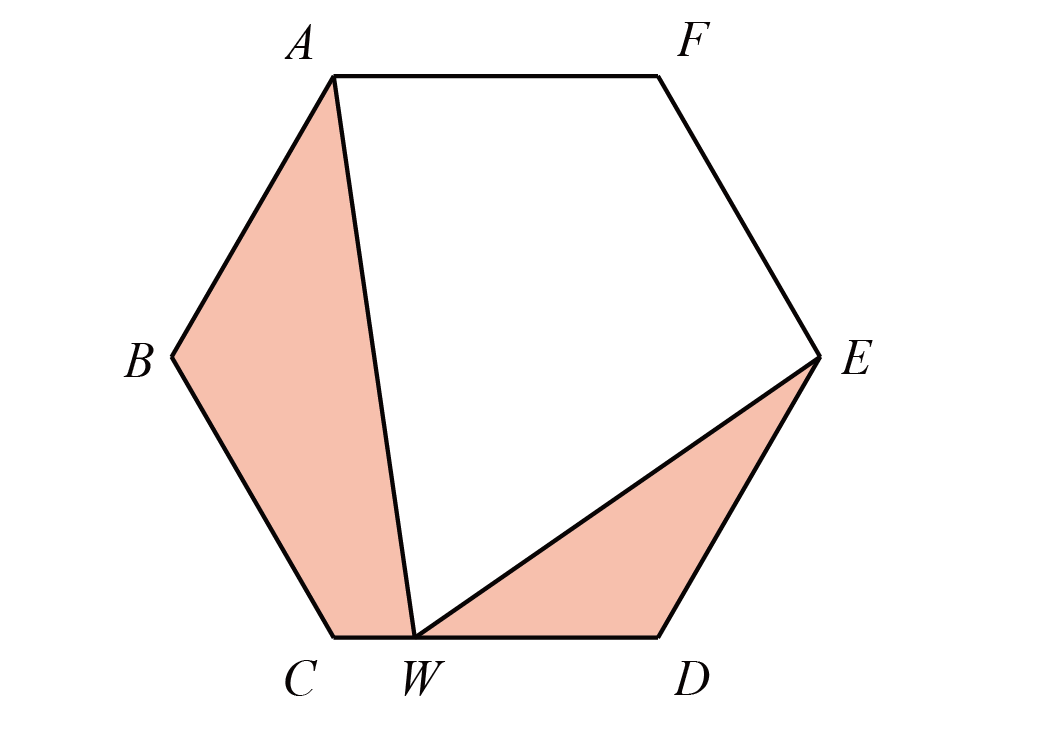
如图，正六边形$ABCDEF$中，$W$是$CD$上一点，已知$S_{BAWC}=2$，$S_{\triangle DWE}=1$，求正六边形$ABCDEF$的面积．

解析

如图，连接$AC$、$CE$，易得$S_{\triangle AWC}=2S_{\triangle EWC}$，则

$$2-S_{\triangle AWC}=1+S_{\triangle EWC}$$

$$2-2S_{\triangle EWC}=1+S_{\triangle EWC}$$

所以

$$S_{\triangle EWC}=\dfrac{1}{3}$$

那么$S_{ABCDEF}=(1+\dfrac{1}{3})\times 6=8$．