【小奥】问题50 已知圆的半径求带状部分的面积

问题

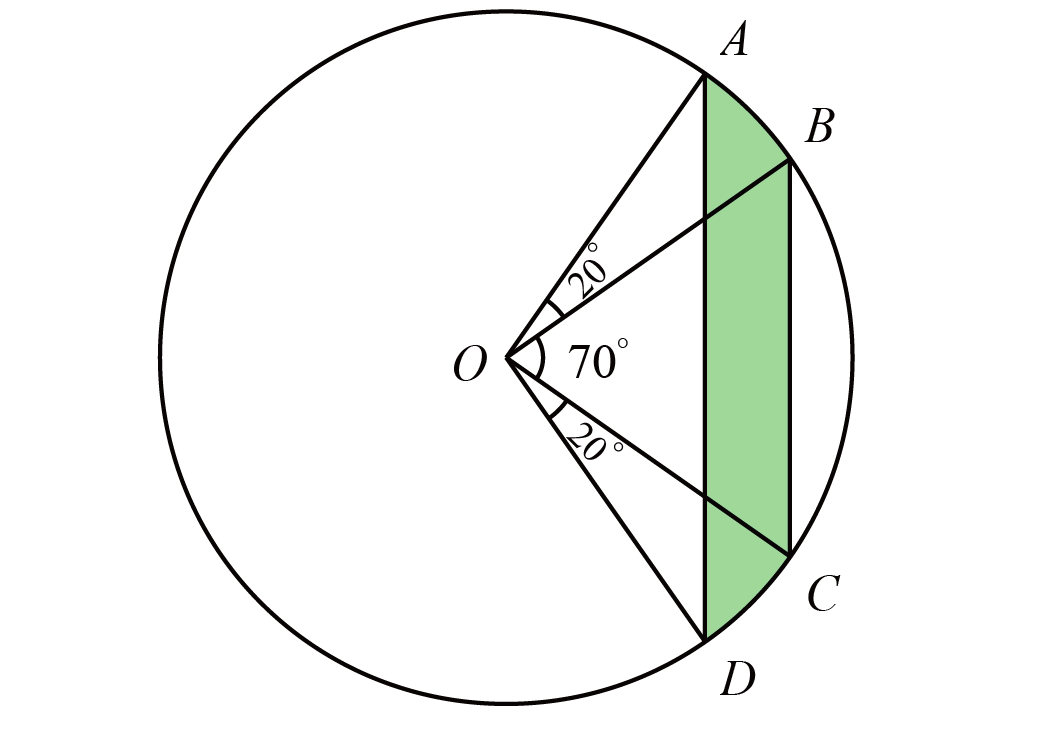
如图，一个圆的半径为$12$，$A$、$B$、$C$、$D$是圆上的点，$O$是圆心，且$\angle AOB=\angle COD=20^{\circ}$，$\angle BOC=70^{\circ}$，求阴影部分的面积．

解析

如图，$\angle AOD=110^{\circ}$，$\angle BOC=70^{\circ}$，所以

$$\angle AOD+\angle BOC=180^{\circ}$$

由鸟头模型易得

$$\dfrac{S_{\triangle AOD}}{S_{\triangle BOC}}=\dfrac{OA\times OD}{OB\times OC}=1$$

所以$S_{\triangle AOD}=S_{\triangle BOC}$，因此阴影部分的面积等于两个$20^{\circ}$的扇形，则

$$S_{阴影}=\dfrac{40}{360}\times \pi\times 12^2=16\pi =50.24$$