【小奥】问题36 正六边形求面积

问题

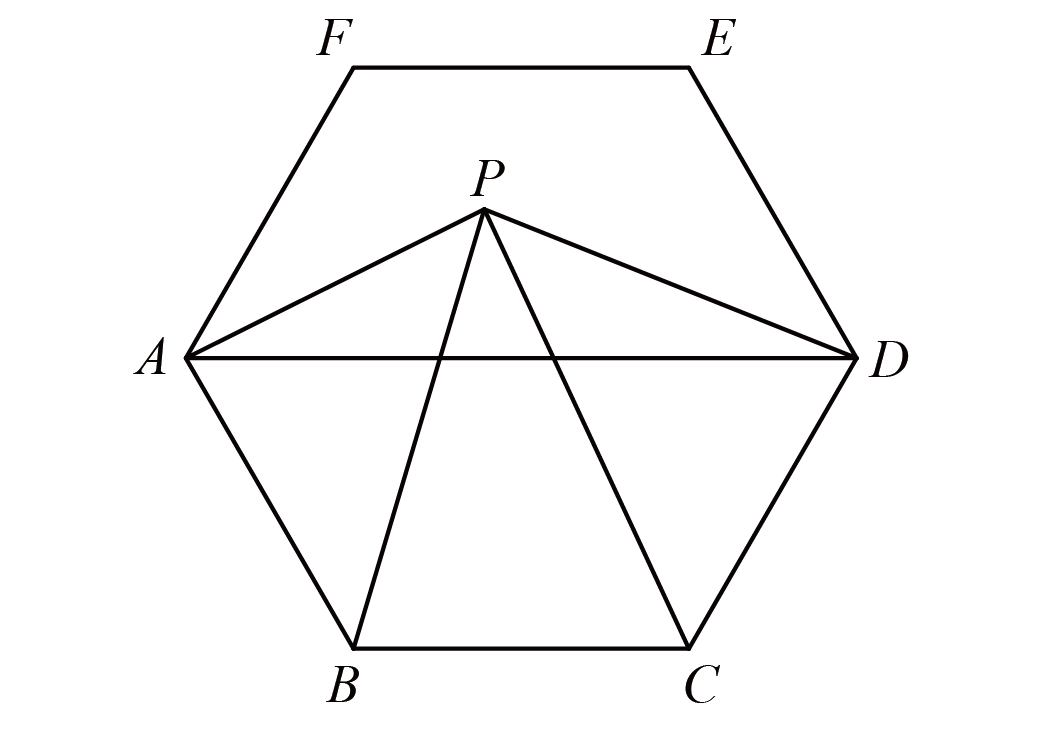
如图，正六边形内$P$点分别与顶点$A$、$B$、$C$、$D$相连，$S_{\triangle PAD}=10$，$S_{\triangle PBC}=12$，那么正六边形的面积是多少？

解析

如图，设$AD$的中点为$O$，连接$OP$、$OB$、$OC$，则$S_{\triangle POD}=10\div 2=5$，由一半模型可得
$$S_{\triangle OBC}=S_{\triangle PBC}-S_{\triangle POD}=12-5=7$$

因此$S_{正六}=6\times 7=42$．