【小奥】问题41 求直角三角形内阴影部分的面积

问题

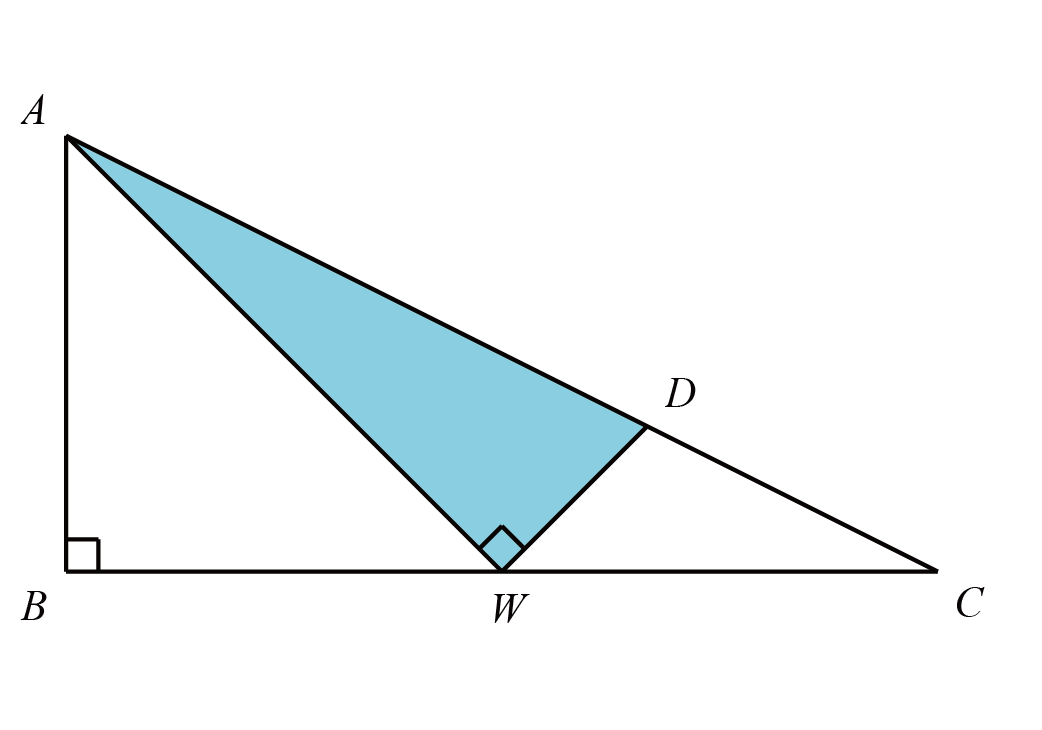
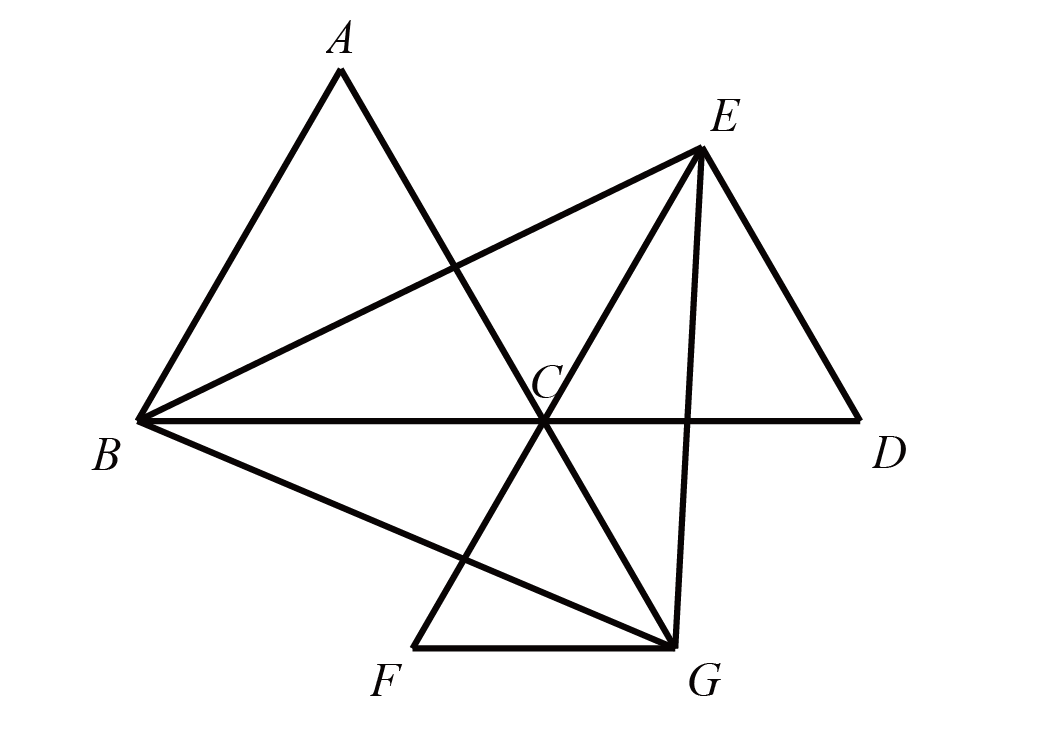
如图，三角形$ABC$是直角三角形，$\angle B=90^{\circ}$，$AB=BW=WC=3$，且$\angle AWD=90^{\circ}$，求阴影部分的面积．

解析

法1

如图，过$D$作$DE\perp WC$于点$E$，设$DE=WE=a$

因为$\dfrac{DE}{EC} =\dfrac{AB}{BC} =\dfrac{3}{6} =\dfrac{1}{2} $

所以$EC=2a$，则$WC=a+2a=3a=3$，那么$a=1$

所以$S_{\triangle AWD} =\dfrac{1}{2} \times 6\times 3-\dfrac{1}{2} \times 3\times 3-\dfrac{1}{2} \times 3\times 1=3$

法2

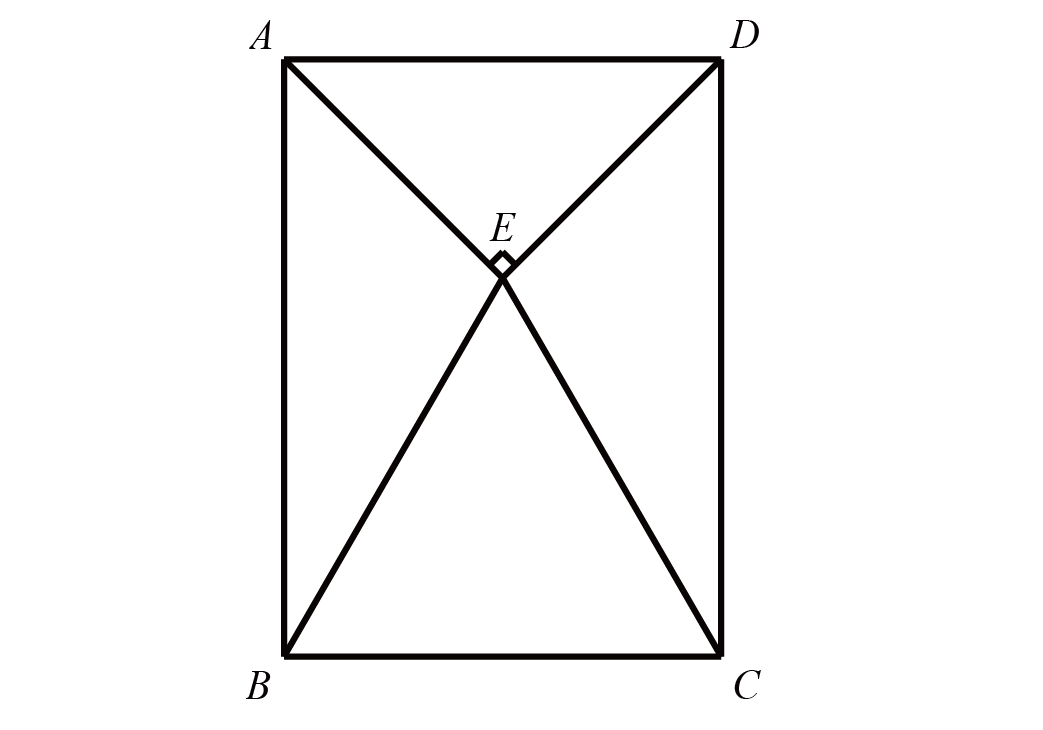
如图，构造长方形$ABCE$，连接$DE$，则$W$、$D$、$E$共线

易得$AD:DC=AE:WC=6:3=2:1$

所以$S_{\triangle AWD} =\dfrac{2}{3} S_{\triangle AWC} =\dfrac{2}{3} \times \dfrac{1}{2} \times 3\times 3=3$