【小奥】问题85 边旋转一周扫过的面积

问题

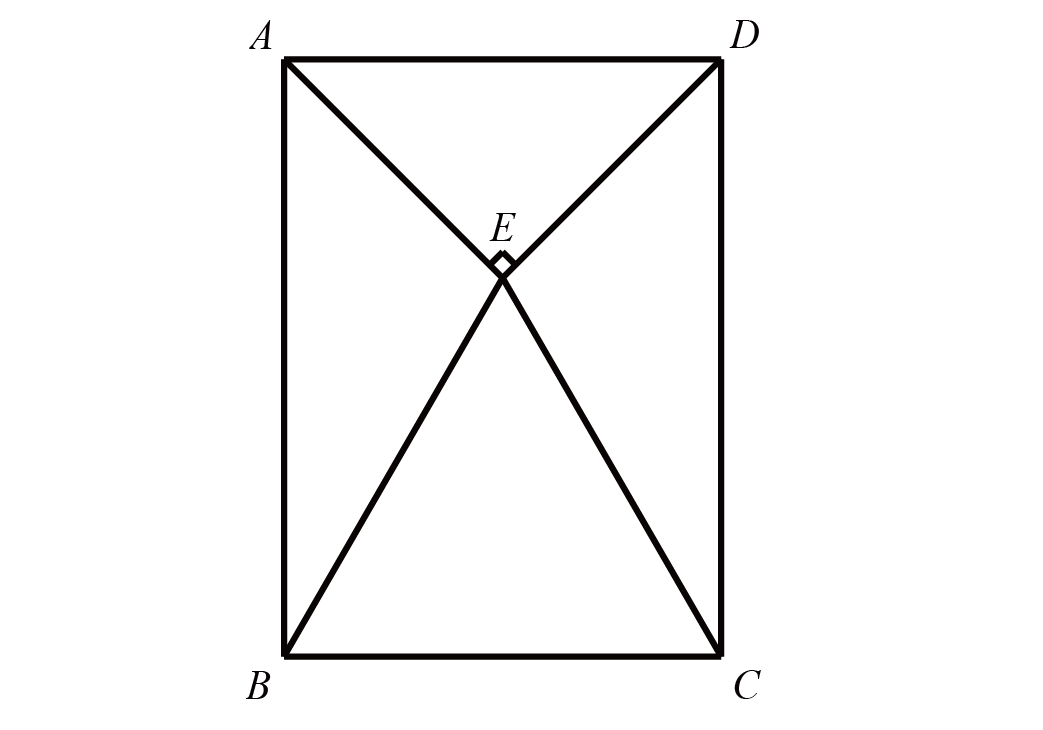
如图$1$所示，在长方形$ABCD$中，$\triangle BEC$是正三角形，$\triangle ADE$是等要直角三角形，已知$DE=5$，现将$\triangle ABE$绕点$E$旋转一周，求边$AB$扫过区域的面积。

解析

如图，$AB$扫过的区域是一个圆环

$r^{2} +r^{2} =5^{2} $，则$r^{2} =\dfrac{25}{2} $

$R=2r$，所以$R^{2} =4r^{2} $

$S=\pi (R^{2} -r^{2} )=3\pi r^{2} =3\pi \times \dfrac{25}{2} =37.5\pi =117.75$