【小奥】问题86 求三角形的面积比

问题

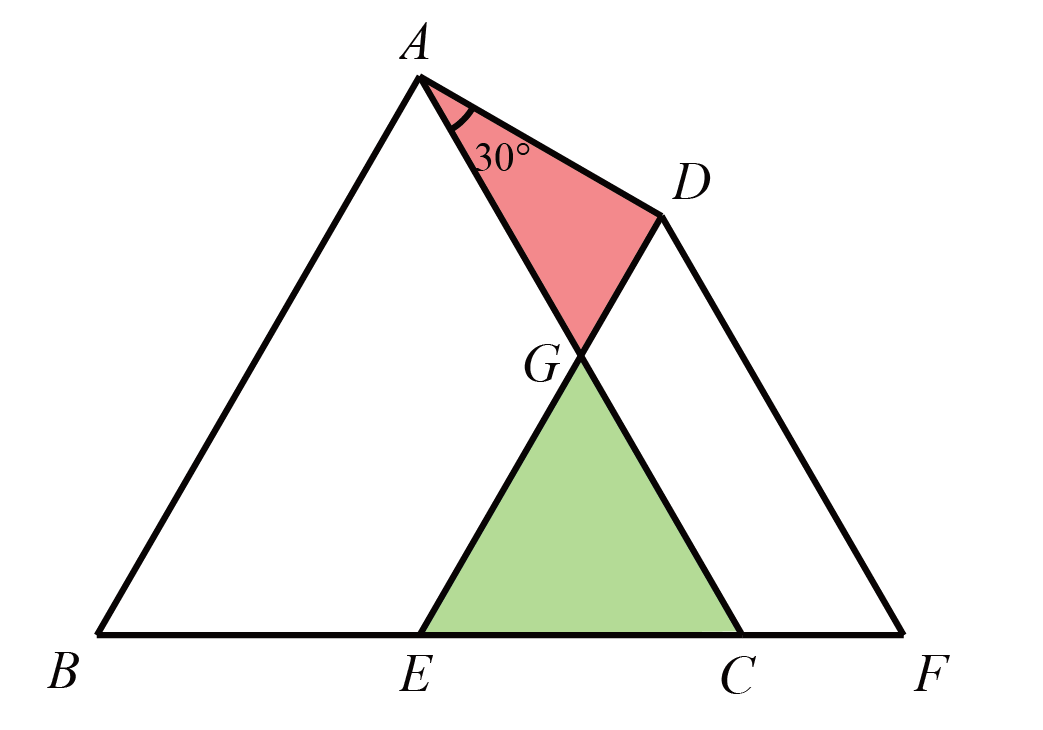
如图所示，有一个边长为$ 4\text{cm} $的等边三角形$ ABC $和一个边长为$ 3\text{cm} $的等边三角形$ DEF$。边$ AC $与边$ DE $相交于点$ G$。已知在$ \triangle AGD $中，$\angle GAD $的大小为$ 30^{\circ}$。求$ \triangle AGD $与$ \triangle GEC $的面积比，并用最简整数比表示。

解析

如图，过$D$作$DH//EF$交$AG$与点$H$

因为$\angle DAH=30^{\circ} $，$\angle DHG=60^{\circ} $，所以$CF=DH=AH=4-3=1$

因此$BG=GC=EC=AG=2$

故$S_{\triangle ADG} :S_{\triangle EGC} =(2\times 1):(2\times 2)=1:2$