【小奥】问题13 正六边形求面积

问题

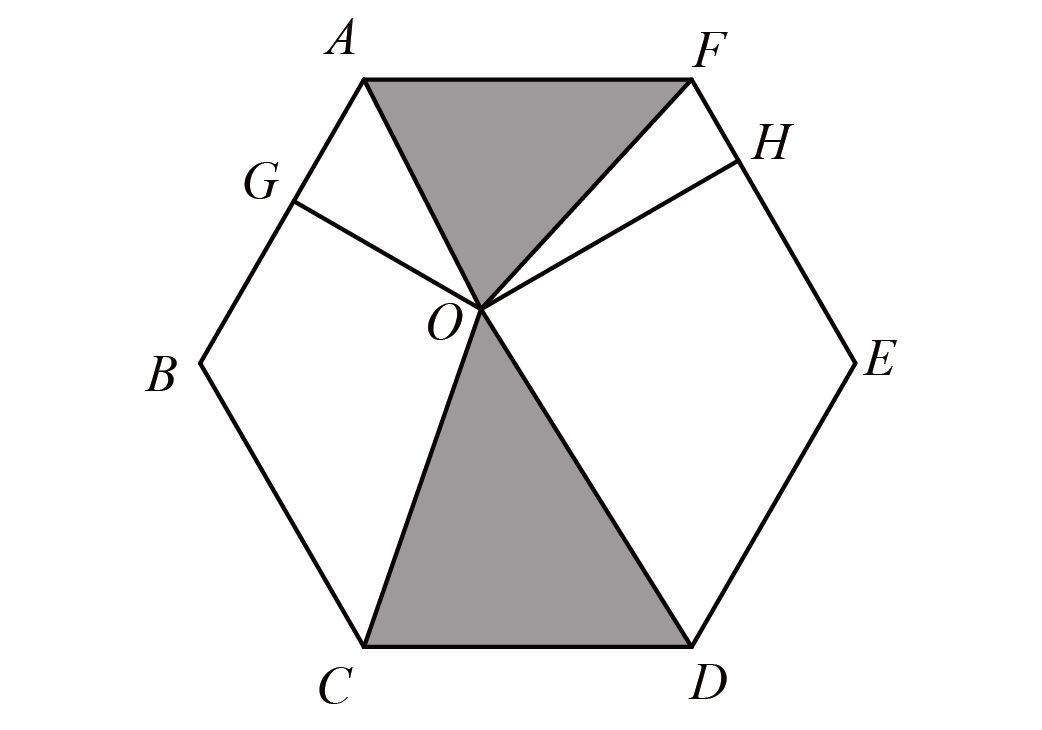
如图，正六边形$ABCDEF$的面积为$1$，$G$是$AB$上一点，$H$是$EF$上一点，且$AG:GB=3:4$，$FH:HE=2:5$，过$G$作$AB$边上的垂线，过$H$作$EF$边上的垂线，两条线交于点$O$，连接$OA$、$OC$、$OD$、$OF$．
(1)求两块阴影部分的面积之和；
(2)求三角形$OCD$的面积．

法1

（1）如图，连接$AC$、$DF$，根据一半模型可得阴影部分的面积为$1\times \dfrac{2}{3}\times \dfrac{1}{2}=\dfrac{1}{3}$．

（2）如图，不妨设正六边形边长为$7$份，后面省略份，由于$\triangle AGW$、$\triangle FHX$、$\triangle BGZ$、$\triangle YHE$都是$60^{\circ}$的直角三角形，所以$AG=3$，$AW=6$，$FH=2$，$FX=4$，$BG=4$，$BZ=8$，$EH=5$，$EY=10$，从而

$$YZ=8+10-14=4$$

$$WX=6+7+4=17$$

故沙漏$WXOYZ$的相似比为$17:4$，所以

$$S_{\triangle AFO}=1\times \dfrac{1}{6}\times \dfrac{17}{17+4}=\dfrac{17}{126}$$
那么$$S_{\triangle OCD}=\dfrac{1}{3}-\dfrac{17}{126}=\dfrac{25}{126}$$

法2：【武汉】邱福星

如图，构造沙漏$PQMN$，不妨设$AG=3$，$FH=2$，则正六边形的边长为$7$，易得

$$AP=2AG=6，FQ=2FH=4$$

所以$$PQ=6+7+4=17$$

同理$$MY=2HY=2\times (5+7)=24$$

$$XN=2XG=2\times (4+7)=22$$

所以$MN=24+22-7\times 3=25$，所以$PQ:MN=17:25$，那么

$$S_{\triangle OCD}=\dfrac{1}{3}\times \dfrac{25}{42}=\dfrac{25}{126}$$

法3：【北京】酒吞

如图，构造大等边三角形$XYZ$，过$O$作$MN$平行于$YZ$，易得

$$MN=2(MG+NH)$$

所以$$MG+MN+NH=\dfrac{3}{2}MN$$

即$GM+MN+NH$是$\triangle XMN$周长的一半，不妨设$AG=3$，$FH=2$，则正六边形的边长为$7$，所以
$$MN=(XG+XH)\times \dfrac{2}{3}=\dfrac{38}{3}$$

所以$\triangle XMN$的高占$\triangle XYZ$高的$\dfrac{38}{3}\div 21=\dfrac{38}{63}$，那么$\triangle OCD$的高占整体的$1-\dfrac{38}{63}=\dfrac{25}{63}$，$\triangle OCD$的底占$YZ$的$\dfrac{1}{3}$，所以

$$S_{\triangle OCD}=\dfrac{1}{3}\times \dfrac{25}{63}\times S_{\triangle XYZ}=\dfrac{1}{3}\times \dfrac{25}{63}\times\dfrac{3}{2}=\dfrac{25}{126}$$

法4：【武汉】邱福星

由上个方法易得$MB=\dfrac{38}{63}YZ$，那么$\triangle OAF$的高占整体的
$$\dfrac{38}{63}\times (1-\dfrac{21}{38})=\dfrac{17}{63}$$

$\triangle OAF$的高占整体的$1-\dfrac{38}{63}=\dfrac{25}{63}$，所以$S_{\triangle AOF}:S_{\triangle COD}=17:25$，故

$$S_{\triangle OCD}=\dfrac{1}{3}\times \dfrac{25}{42}=\dfrac{25}{126}$$

法5：【上海】石头

如图，点$O$从点$D$运动到$F$的过程中，$\triangle OCD$的面积从$0$增加到$\dfrac{1}{3}$，拆解为从$D$到$B$到$F$，两次面积分别增加$\dfrac{1}{6}$、$\dfrac{1}{3}-\dfrac{1}{6}=\dfrac{1}{6}$，又因为

$$HJ:HF=17:4，BG:GI=8:13$$

因此
$$S_{\triangle OCD}=\dfrac{1}{6}\times \dfrac{17}{21}+\dfrac{1}{6}\times \dfrac{8}{21}=\dfrac{25}{126}$$

法6：【北京】胡浩

如图，易得
$$S_{\triangle OAB}=\dfrac{1}{3}\times \dfrac{8}{21}=\dfrac{8}{63}$$

$$S_{\triangle OEF}=\dfrac{1}{3}\times \dfrac{11}{21}=\dfrac{11}{63}$$

所以$$S_{\triangle OCD}=\dfrac{1}{2}- \dfrac{8}{63}-\dfrac{11}{63}=\dfrac{25}{126}$$