【小奥】问题46 已知四边形面积求五边形面积

问题

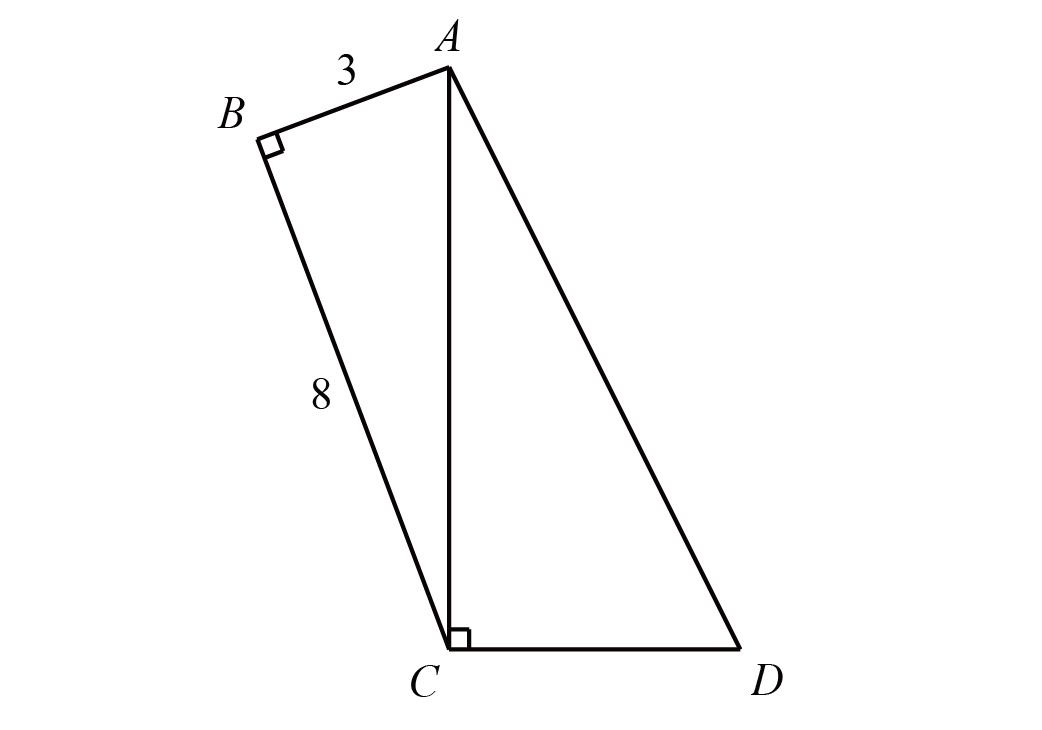
如图，四边形$ABCD$中，$\angle A=\angle C=90^{\circ}$，$E$是$AD$边上一点，$F$是$CD$边上一点，且$\angle EFD=90^{\circ}$，$AB=DF=2$，$CF=3$，已知四边形$ABCD$的面积是$63$，求五边形$ABCFE$的面积．

解析

如图，延长$CB$、$DA$交于点$W$

设$EF=AW=a$，则$S_{\triangle DEF} =S_{\triangle ABW} =2\times a\div 2=a$

又因为$DF:DC=2:5$，所以$S_{\triangle DEF} :S_{\triangle DWC} =4:25$

那么$S_{\triangle DWC} =\dfrac{25}{4} a$，从而$S_{ABCFE} = \dfrac{25}{4} a-a-a=\dfrac{17}{4} a$

因此$S_{ABCD} = \dfrac{17}{4} a+a=\dfrac{21}{4} a=63$，$a=12$

所以$S_{ABCFE} =\dfrac{17}{4} \times 12=51$