【小奥】问题63 两个直角三角形求面积（2022日奥赛）

问题

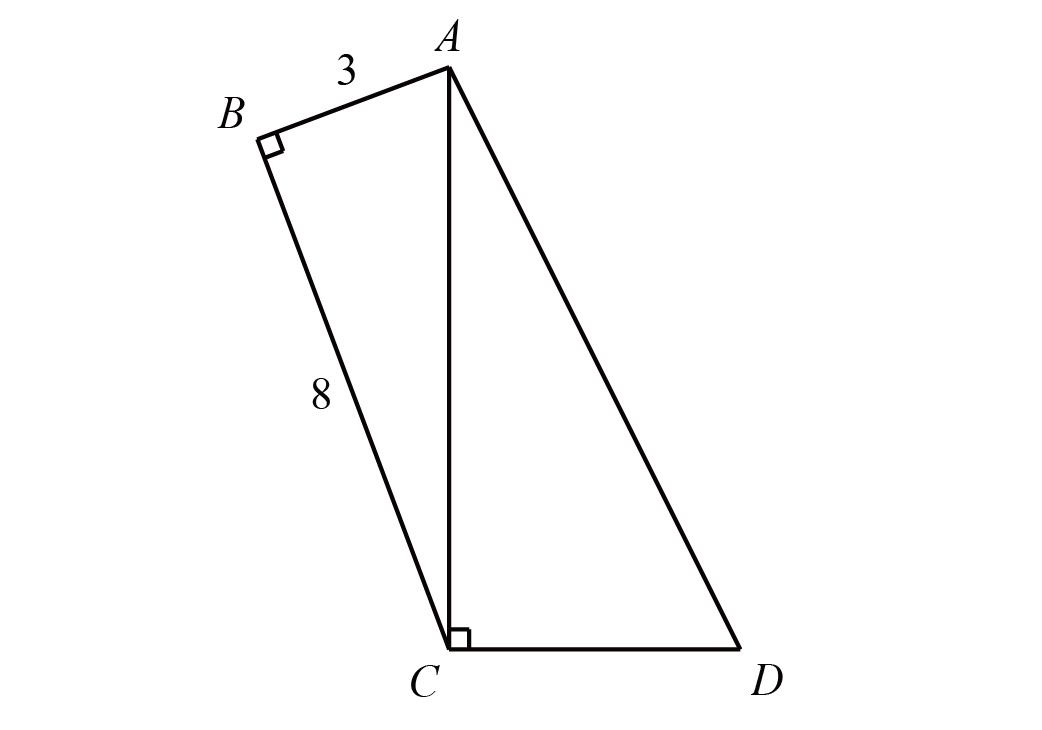
如图，四边形$ABCD$中，$\angle B= \angle ACD=90^{\circ}$，且$AC=2CD$，已知$AB=3$，$BC=8$，求四边形$ABCD$的面积

法1

设$CD=a$，则$AC=2a$，由勾股定理可得$AC^2=AB^2+BC^2$，即

$$(2a)^2=3^2+8^2$$

因此$$4a^2=73$$

那么$$a^2=\dfrac{73}{4}$$

从而
$$\begin{aligned}
S_{ABCD} &=\dfrac{1}{2}\times 3\times 8 + \dfrac{1}{2}a\times (2a) \\
&=12+a^2 \\
&=12+\dfrac{73}{4} \\
&=30.25
\end{aligned}$$

法2

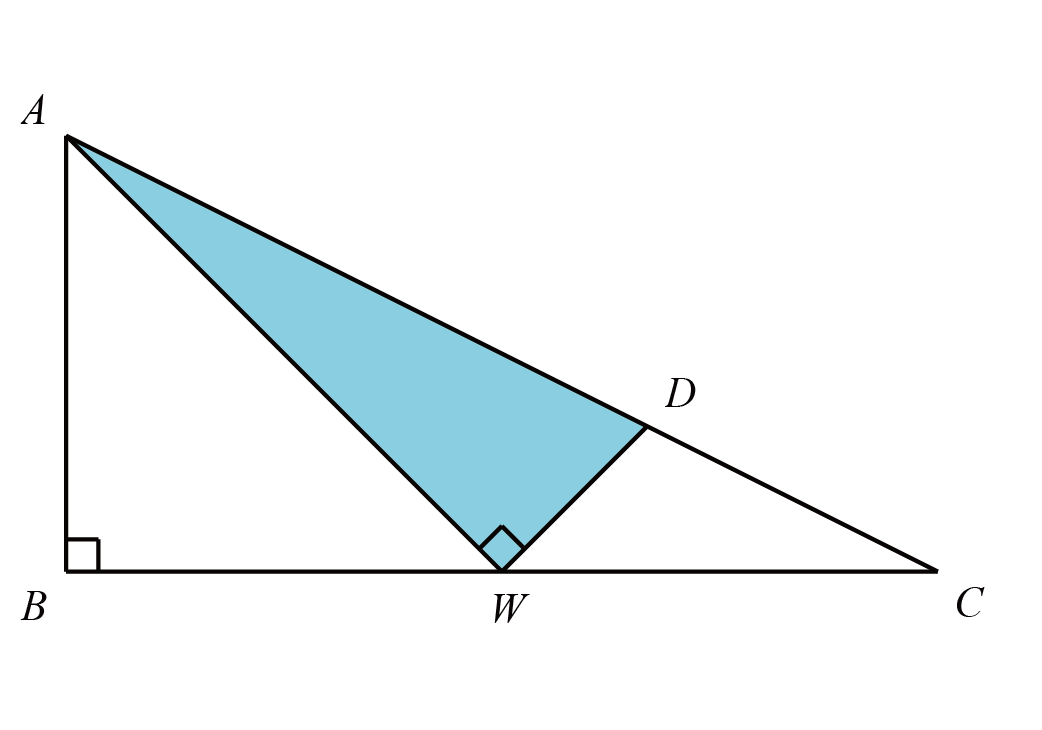
如图构造弦图，易得$S_{ABCD}=(3+8)^2\div 4 =30.25$