【小奥】问题48 三个等边三角形求阴影部分面积

问题

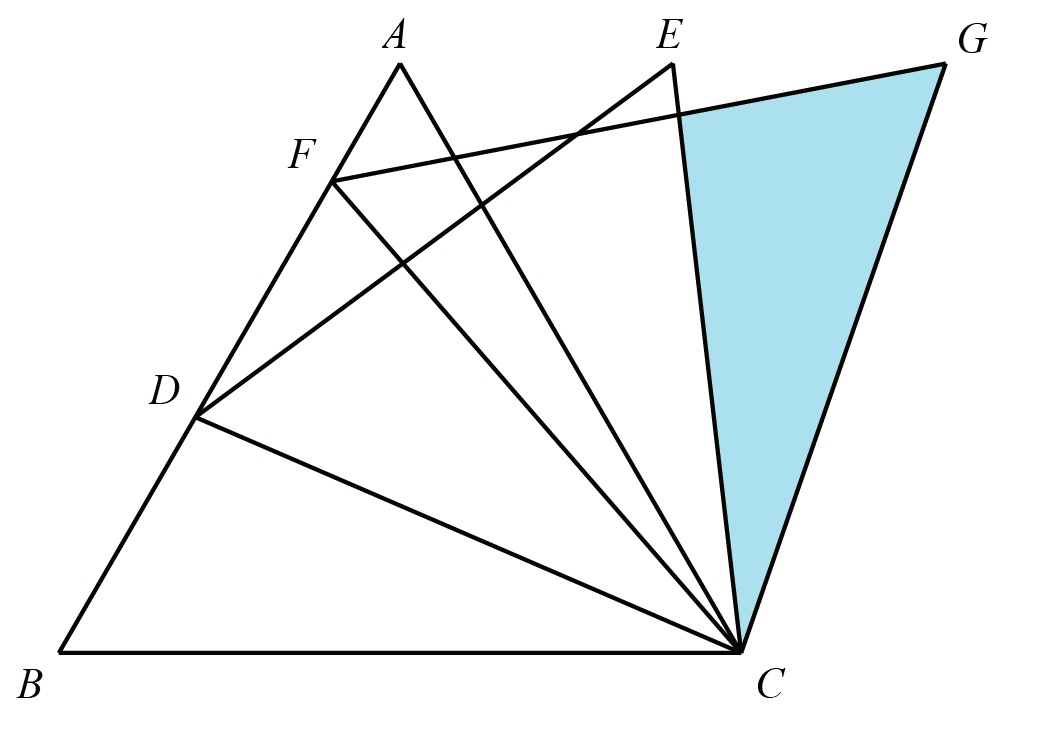
如图，$\triangle ABC$、$\triangle CDE$、$\triangle CFG$都是等边三角形，$AF:FD:DB=1:2:2$，已知$\triangle ABC$的面积是$125$，分别求图中两个阴影部分的面积．

解析

(1)如图构造大的正$\triangle PBW$，连接$AE$，则

$$PD:DB=BC:WC=WE:EP=5:2$$

由鸟头模型易得$$S_{\triangle CDE}=1-\dfrac{5}{7}\times \dfrac{2}{7}\times 3=\dfrac{19}{49}S_{\triangle BPW}$$

又$BC:BW=5:7$，所以$S_{\triangle ABC}:S_{\triangle BPW}=25:49$，因此

$$S_{\triangle BPW}=125\times \dfrac{49}{25}=245$$

那么$$S_{\triangle CDE}=245\times \dfrac{19}{49}=95$$

又因为$BC=AC$，$DC=EC$，$\angle BCD=ACE$，$\triangle ACE$相当于由$\triangle BCD$顺时针旋转$60^{\circ}$所得，那么

$$DO:OE=S_{\triangle ADC}:S_{\triangle ACE}=S_{\triangle ADC}:S_{\triangle BCD}=AD:DB=3:2$$

所以$S_{阴影}=95\times \dfrac{2}{5}=38$．

(2)如图，由沙漏模型易得$EH:HC=2:21$，由旋转易得

$$S_{\triangle CEG}=S_{\triangle CDF}=125\times \dfrac{2}{5}=50$$

所以$S_{阴影}=50\times \dfrac{21}{23}=\dfrac{1050}{23}$．