题目

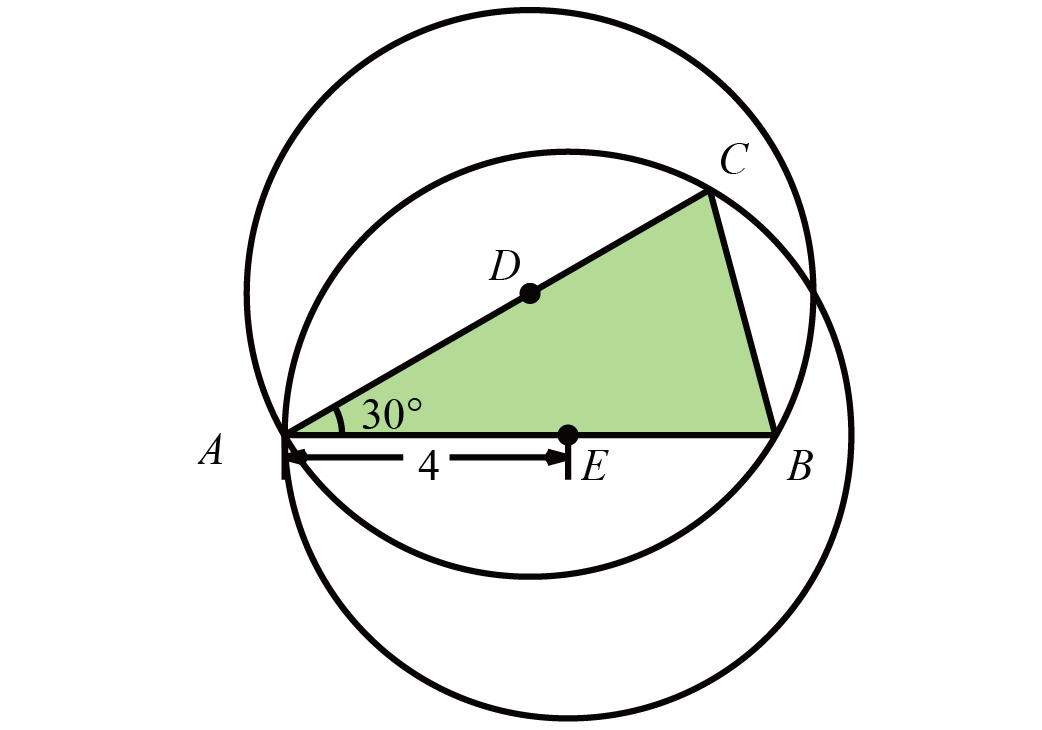
如图，两个半径为4的圆的圆心分别是$D$、$E$，且$\angle BAC=30^{\circ}$，求阴影三角形$ABC$的面积。

解答

如图，连接$BD$、$CE$

因为$\angle DAE=30^{\circ}$，$AE=AD=DB=EC$

所以$\angle ADE=\angle AED=75^{\circ}$，$\angle ECA=\angle DBA=30^{\circ}$

从而$\angle AEC=\angle ADB=120^{\circ}$

因此$\angle CED=\angle BDE=45^{\circ}$

那么$CE\perp BD$，故

$$
\begin{align}
S_{\triangle ABC}&=S_{\triangle ADE}+S_{BCDE} \\
&=\dfrac{1}{2}\times 4\times 2 + \dfrac{1}{2}\times 4\times 4 \\
&=4+8 \\
&=12
\end{align}
$$