【小奥】问题66 两个半圆求阴影部分面积

题目

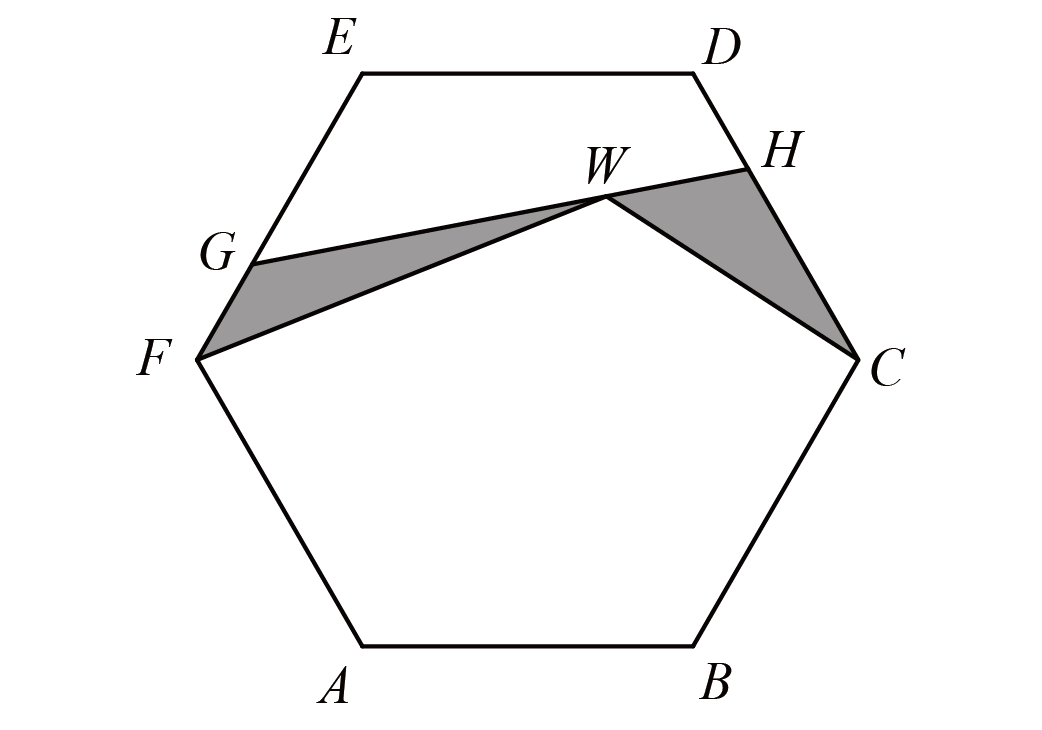
如图，长方形$ABCD$中，有两个半径为$6$的半圆，求阴影部分的面积

解答

如图，连接$EF$、$FG$、$GE$、$EI$、$EH$

因为$EF=FG=GE$，所以$\triangle EFG$是正三角形，则$\angle GEF=60^{\circ}$

从而$\angle BEG=90^{\circ}-60^{\circ}=30^{\circ}$，$\angle GEC=180^{\circ}-30^{\circ}=150^{\circ}$

因为$GE=EC$，所以$\angle EGC=(180^{\circ}-150^{\circ})\div 2=15^{\circ}$

同理$\angle FGD=15^{\circ}$，那么$\angle HGI=30^{\circ}$

根据等积变形，$S_{\triangle GHI}=S_{\triangle GEI}=6\times 6\div 2=18$