题目

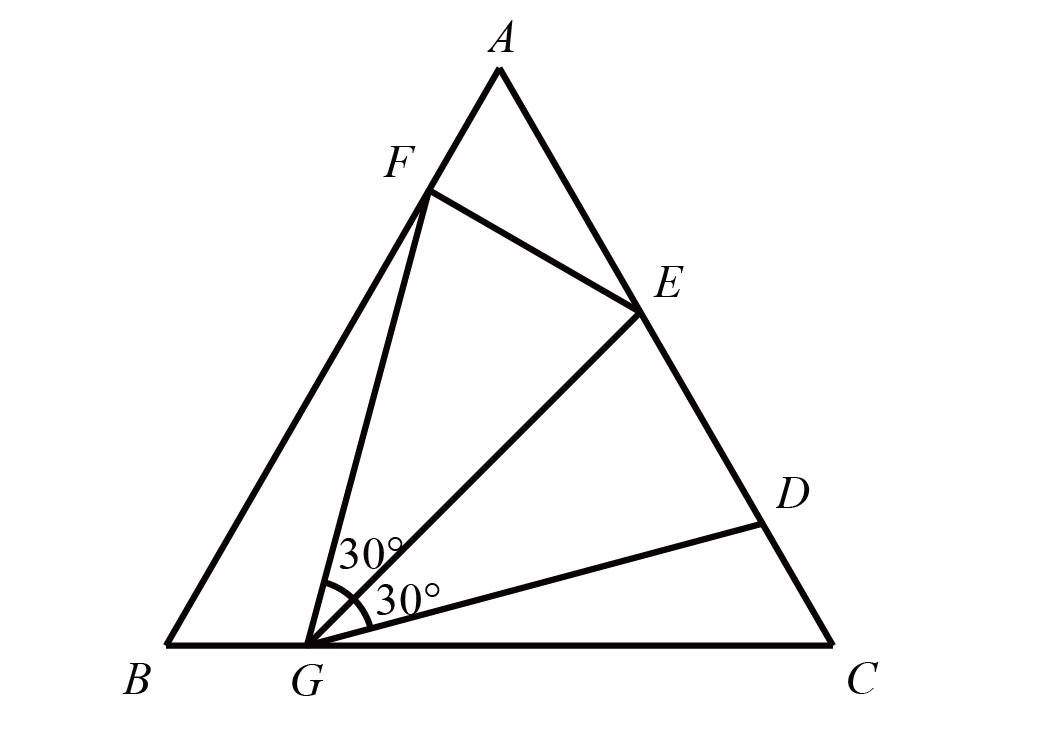
如图，正三角形$\triangle ABC$中，$FG=EG=DG$，$\angle FGE=\angle DGE =30^{\circ}$，$AE=24$，求$CD$的长度

解答

连接$DF$，因为$FG=DG$，$\angle FGD=60^{\circ}$，所以$\triangle DFG$是正三角形，根据三角弦图可知$CD=AF$

因为$\angle GEF=\angle GED=(180^{\circ}-30^{\circ})\div 2 = 75^{\circ}$，所以$\angle AEF=180^{\circ}-75^{\circ}\times 2 = 30^{\circ}$，所以$AF=AE\div 2 = 12$。