【小奥】问题16 正六边形求边长比

问题

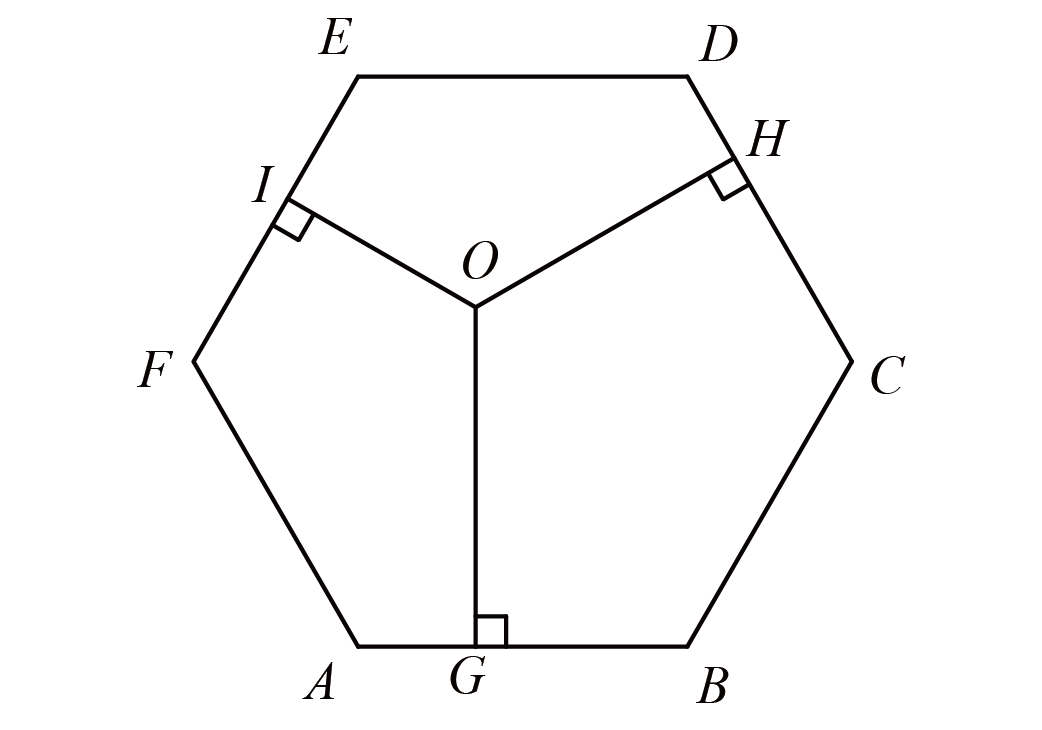
如图，正六边形内部有一个点$O$，$OG$、$OH$、$OI$分别和$AB$、$CD$、$EF$垂直，已知$EI:IF=3:4$，$AG:GB=5:9$，求$CH:HD$．

解析

法1

如图，在正三角形$ABC$中，$O$是内部任意点，过$O$作三条边上的高，则

$$\begin{align} AE+BF+CD &= 2c+a+2a+b+2b+c \\ &= 3(a+b+c) \\ &= BE+CF+AD \end{align} $$

将$AB$、$CD$、$EF$分别向两边延长，得到正三角形$MNL$，因为$EI:IF=3:4$，$AG:GB=5:9$，设$EI=6a$，$IF=8a$，则$AG=5a$，$BG=9a$

$$\begin{align} NI+LG+NH &= 20a+19a+14a+CH \\ &= 14a\times 9\times \dfrac{1}{2} \end{align} $$
所以$CH=10a$，所以$DH=14a-10a=4a$，所以$CH:HD=10a:4a=5:2$．

法2

如图，连接$AE$、$EC$、$CA$，过$O$分别向三角形$ACE$三条边作高，过$C$作$CP$垂直$AE$于点$P$，所以

$$EI+AG+CH=OL+OM+ON=CP=\dfrac{3}{4}\times 2AB=1.5AB$$

所以$$EI+AG+CH=FI+BG+DH$$

因为$EI:IF=3:4$，$AG:GB=5:9$，设$EI=6a$，$IF=8a$，则$AG=5a$，$BG=9a$，则$$6a+5a+CH=1.5AB=21a$$

所以$CH=10a$，$DH=14a-10a=4a$，故$$CH:HD=10a:4a=5:2$$