问题
如图,正六边形外面连接着三个正方形,已知$HI=4$,求阴影部分的面积.
解析
如图,$HABIM$是正十二边形的$\dfrac{1}{4}$,设$MH=R$,根据勾股定理可得$R^{2}+R^{2}=4^2$
所以$R^{2}=8$,故阴影部分的面积为$\left( \dfrac{3}{4}R^{2}-\dfrac{1}{2}R^{2} \right) \times 3=6$.
© 版权声明
部分题目来自网络,如有侵权,请联系删除
THE END
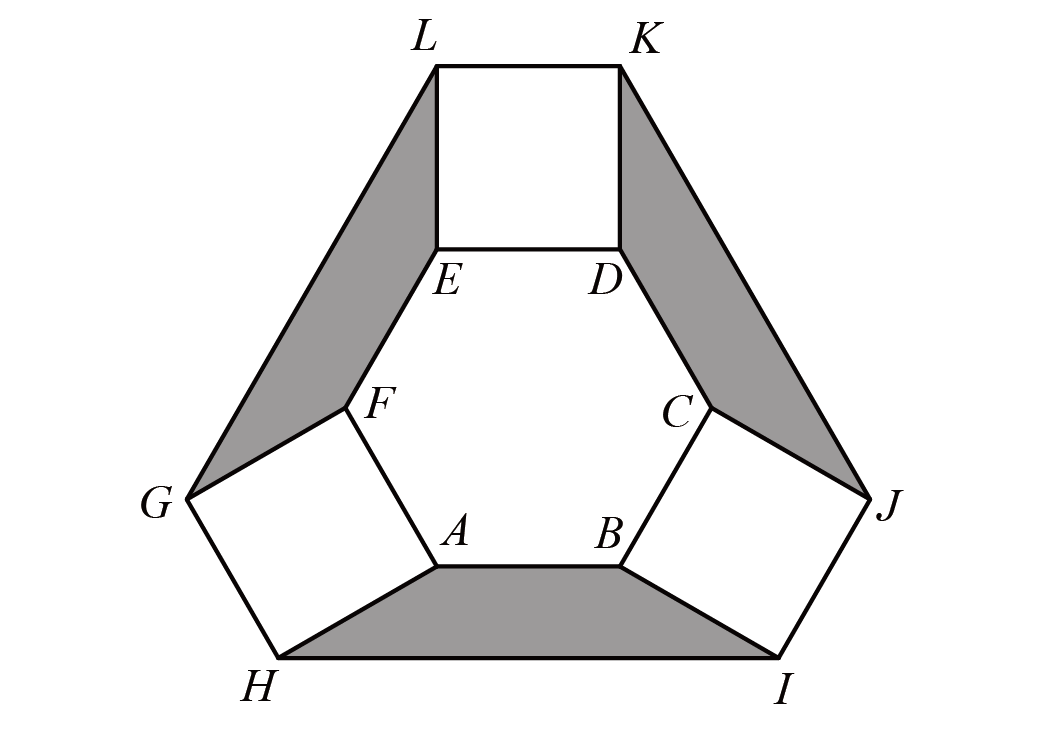
如图,正六边形外面连接着三个正方形,已知$HI=4$,求阴影部分的面积.
如图,$HABIM$是正十二边形的$\dfrac{1}{4}$,设$MH=R$,根据勾股定理可得$R^{2}+R^{2}=4^2$
所以$R^{2}=8$,故阴影部分的面积为$\left( \dfrac{3}{4}R^{2}-\dfrac{1}{2}R^{2} \right) \times 3=6$.
暂无评论内容