【小奥】问题52 直角三角形内阴影部分的面积

问题

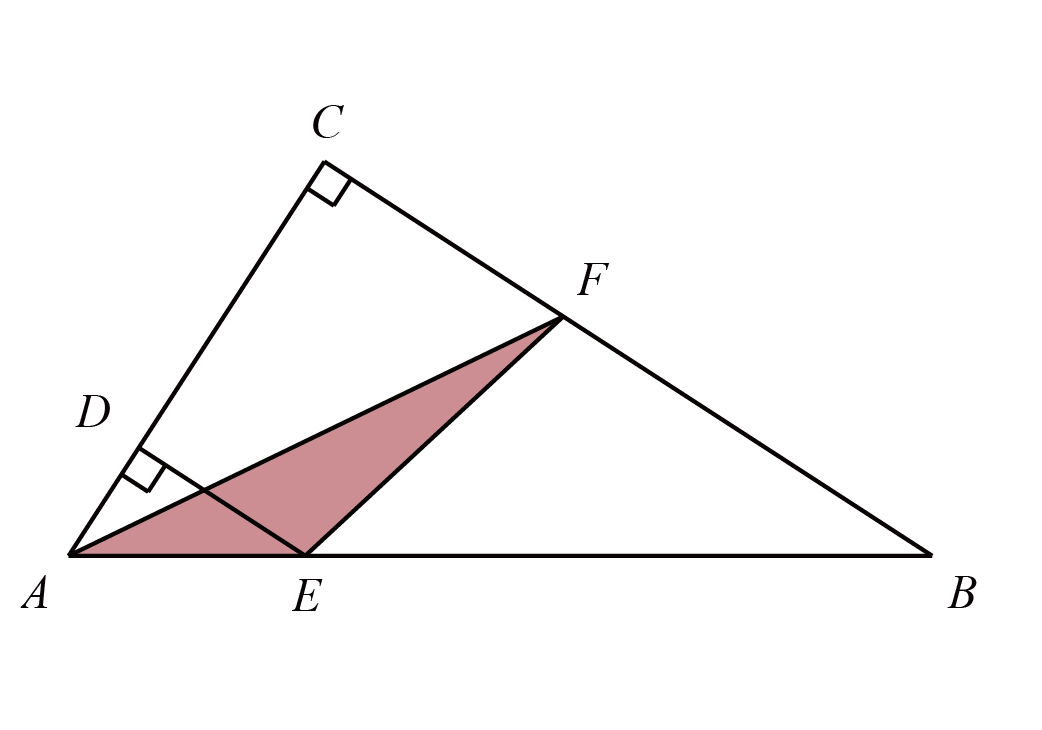
如图，直角$\triangle ABC$中，$\angle C=90^{\circ}$，$DE$和$BC$平行，$F$是$BC$上一点，已知$AD=2$，$BF=5$，求阴影部分的面积．

法1

割补法，由整体减空白易得：

$$\begin{aligned}
S_{\triangle AEF}&=S_{\triangle ABF}-S_{\triangle BEF}& \
&=\dfrac{1}{2}\times BF\times AC-\dfrac{1}{2}\times BF\times DC \
&=\dfrac{1}{2}\times BF\times (AC-DC) \
&=\dfrac{1}{2}\times BF\times AD \
&=\dfrac{1}{2}\times 5 \times 2 \
&=5
\end{aligned}$$

法2

如图，在$AB$上取点$P$，使得$BP=AE$，过$P$作$PQ$垂直$BF$于点$Q$．

易得

$$PQ=AD=2$$

所以

$$S_{\triangle AEF}=S_{\triangle BPF}=\dfrac{1}{2}\times 5\times 2=5$$

法3

如图，过点$F$作$PF$平行$AB$交$ED$的延长线于点$P$，连接$AP$．

易得

$$PE=BF=5$$

所以

$$S_{\triangle AEF}=S_{\triangle PAE}=\dfrac{1}{2}\times 5\times 2=5$$

法4

如图，由相似模型易得

$$\dfrac{AD}{AC}=\dfrac{AP}{AF}=\dfrac{PE}{BF}$$

所以

$$PE\times AC=BF\times AD$$

因此

$$S_{\triangle AEF}=\dfrac{1}{2}\times PE\times AC=\dfrac{1}{2} \times BF\times AD=\dfrac{1}{2}\times 5\times 2=5$$

法5

如图，过点$F$作$FP$垂直$AB$于点$P$，易得$\triangle ADE\sim \triangle FPB$

所以

$$\dfrac{AD}{FP}=\dfrac{AE}{FB}$$

故

$$AE\times FP=BF\times AD$$

所以

$$S_{\triangle AEF}=\dfrac{1}{2}\times AE\times FP=\dfrac{1}{2}\times BF\times AD=\dfrac{1}{2}\times 5\times 2=5$$