2022-2023学年度武汉市部分学校九年级调考第23题（四调）

问题

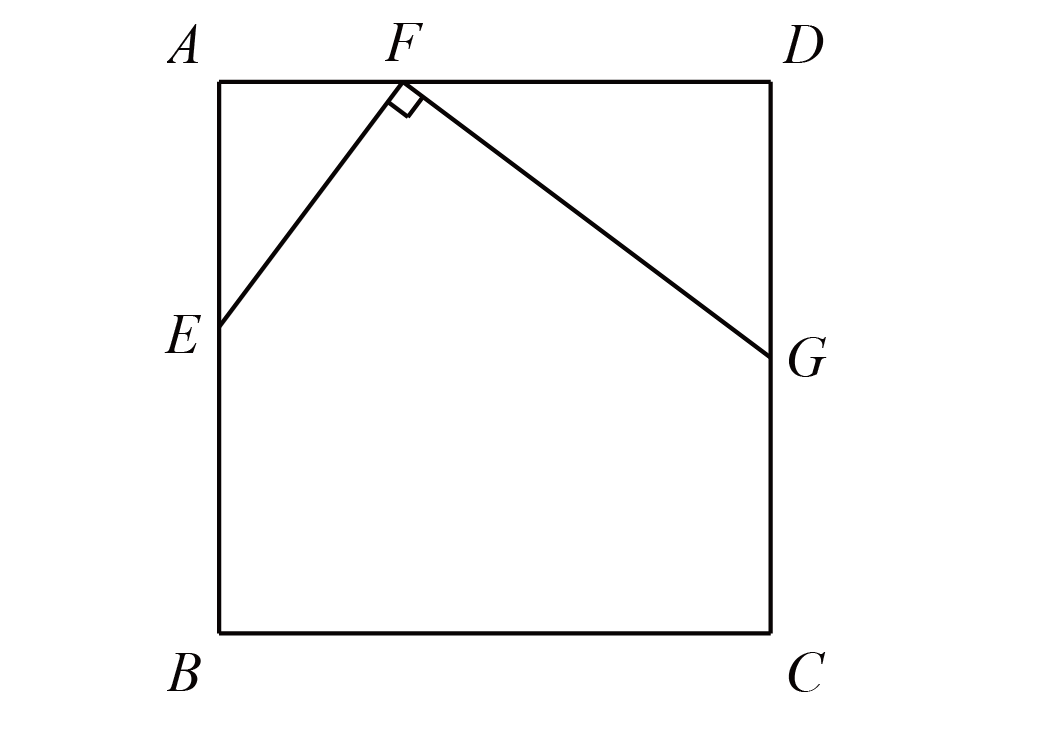
探索发现 如图 (1)$E$, $F$, $H$ 是正方形 $ABCD$ 边上的点, 连接 $BE$, $CF$ 交于点 $G$ 、连接 $AG$, $GH$, $CE=DF$.
(1) 判断 $BE$ 与 $CF$ 的位置关系, 并证明你的结论;
(2) 若 $CE=CH$, 求证: $\mathrm{\angle }BAG=\mathrm{\angle }CHG$.

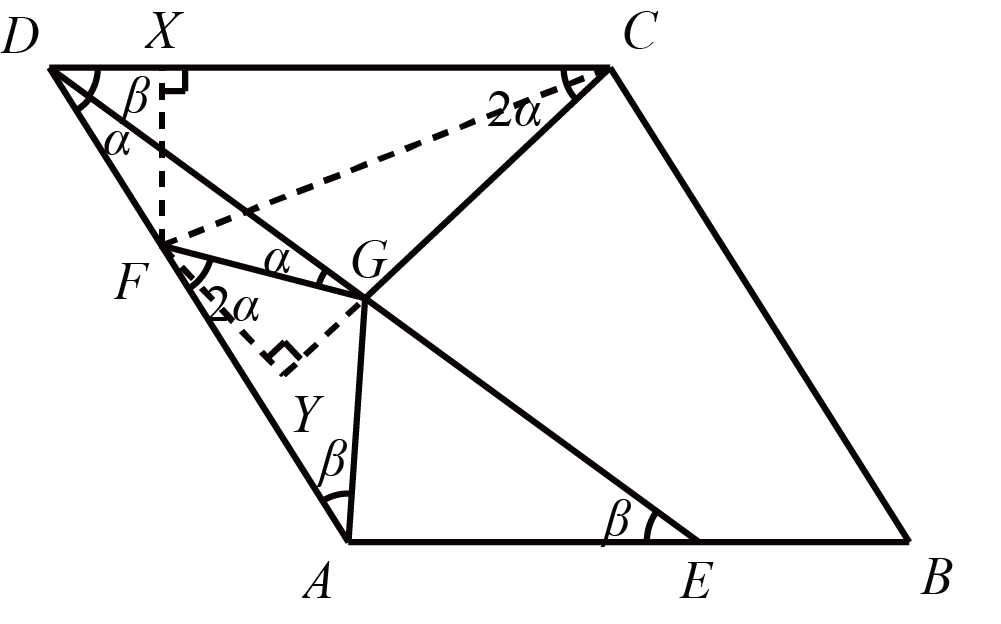
迁移拓展 如图 (2), $E,F$ 是菱形 $ABCD$ 边 $AB$, $AD$ 上的点, 连接 $DE$, 点 $G$ 在 $DE$ 上, 连接 $AG$, $FG$, $CG$, $\mathrm{\angle }AGD=\mathrm{\angle }BAD$, $AF=AE$, $DF=GF$, $CD=10$, $CG=6$, 直接写出 $DF$ 的长及 $\cos \mathrm{\angle }ADC$ 的值.

解答

（1）$BE\mathrm{\perp }CF$，因为$DF=CE$，$\mathrm{\angle }FDC=\mathrm{\angle }ECB={90}^{\circ }$，$DC=CB$，所以$\mathrm{△}DCF\cong \mathrm{△}ECB$，故$\mathrm{\angle }DCF=\mathrm{\angle }CBE$，所以$\mathrm{\angle }CBE+\mathrm{\angle }BCG=\mathrm{\angle }DCF+\mathrm{\angle }BCG={90}^{\circ }$，因此$BE\mathrm{\perp }CF$

（2）由（1）得$\mathrm{\angle }HCG+\mathrm{\angle }CBG=\mathrm{\angle }CBG+\mathrm{\angle }ABG={90}^{\circ }$，所以$\mathrm{\angle }HCG=\mathrm{\angle }ABG$，又因为${\displaystyle \frac{AB}{HC}}={\displaystyle \frac{BC}{CE}}={\displaystyle \frac{BG}{GC}}$，那么$\mathrm{△}ABG\sim \mathrm{△}HCG$，所以$\mathrm{\angle }BAG=\mathrm{\angle }CHG$

（3）因为$\mathrm{\angle }AGD=\mathrm{\angle }EAD$，则$\mathrm{△}DAG\sim \mathrm{△}DEA$，所以$\mathrm{\angle }FAG=\mathrm{\angle }AED=\mathrm{\angle }CDG$，${\displaystyle \frac{AE}{AD}}={\displaystyle \frac{AG}{DG}}$
又因为$${\displaystyle \frac{AF}{CD}}={\displaystyle \frac{AE}{AD}}={\displaystyle \frac{AG}{DG}}$$
所以$$\mathrm{△}FAG\sim \mathrm{△}CDG$$
所以$${\displaystyle \frac{AF}{FG}}={\displaystyle \frac{CD}{CG}}={\displaystyle \frac{10}{6}}={\displaystyle \frac{5}{3}}$$
故${\displaystyle \frac{AF}{FD}}={\displaystyle \frac{5}{3}}$，因此$DF=10\times {\displaystyle \frac{3}{8}}={\displaystyle \frac{15}{4}}$

如图，连接$CF$，过$F$作$FX\mathrm{\perp }CD$于$X$，过$F$作$FY\mathrm{\perp }CG$于$Y$，设$\mathrm{\angle }FDG=\mathrm{\angle }FGD=\alpha$，则$\mathrm{\angle }DCG=\mathrm{\angle }AFG=2\alpha$，所以四边形$CDFG$对角互补，即$C$、$D$、$F$、$G$四点共圆，又因为$DF=FG$，所以$\mathrm{\angle }DCF=\mathrm{\angle }GCF$，所以$FX=FY$，则
$$Rt\mathrm{\angle }FDX\cong Rt\mathrm{△}FGY$$
所以$$DX=YG={\displaystyle \frac{1}{2}}(CD-CG)={\displaystyle \frac{1}{2}}(10-6)=2$$
故$$\cos \mathrm{\angle }ADC={\displaystyle \frac{DX}{DF}}={\displaystyle \frac{2}{{\displaystyle \frac{15}{4}}}}={\displaystyle \frac{8}{15}}$$