2022-2023学年度武汉市部分学校九年级调研考试（二调）-邱福星的教学页面

武汉市教育科学研究院命別
2023.2.21
亲爱的同学,在你答题前,请认真阅读下面的注意事项：

本试卷由第 I 卷 (选择题) 和第 II 卷(非选择题) 两部分组成. 全卷共 6 页, 三大题, 满分 120 分, 考试用时 120 分钟.
答题前, 请将你的妵名、淮考证号填写在“笒题卡”相应位置, 并在“答题卡”背面左上角填写姓名和座位号.
答第 I 卷 (选择题) 时, 选出每小题答案后, 用 $2 \mathrm{B}$ 铅笔把 “答题卡”上对应题目的答案标号涂黑. 如需改动, 用㯃皮擦干净后, 再选涂其他答案. 答在“试卷”上无效.
答第 II 卷(非选择题) 时,答案用 $0.5$ 毫米黑色笔迹签字笔书写在“答题卡”上. 答在“试卷”上无放.
认真阅读答戛卡上的注意事项.预祝你取得优异成绩!

第 I 卷(选择题共 30 分)

一、选择题(共 10 小题, 每小题 3 分, 共 30 分)

下列各题中有且只有一个正确答案, 请在答题卡上将正确答案的标号涂黑.

“守枺待兔”这个事件是($\qquad$)
A. 随机事件
B. 确定性事件
C. 必然事件
D. 不可能事件
下列图形是中心对称图形的是($\qquad$)
A.
B.
C.
D.
解一元二次方程 $x^{2}-2 x-4=0$, 配方后正确的是($\qquad$)
A. $(x-1)^{2}=3$
B. $(x-1)^{2}=4$
C. $(x-1)^{2}=5$
D. $(x-2)^{2}=8$
已知一元二次方程 $x^{2}+4 x-1=0$ 的两根分别为 $m, n$, 则 $m n-m-n$ 的值是($\qquad$)
A. 5
B. 3
C. $-3$
D. $-5$
如图, 已知 $\odot O$ 的半径为 5 , 直线 $A B$ 经过 $\odot O$ 上一点 $P$, 下列条件不能判定直线 $A B$ 与 $\odot O$ 相切的是($\qquad$)

A. $O P=5$
B. $\angle A P O=\angle B P O$
C. 点 $O$ 到直线 $A B$ 的距离是 5
D. $O P \perp A B$
某品牌手机原来每部售价为 1999 元, 经过连续两次降价后, 该手机每部售价为 1360 元, 设平均每次降价的百分率为 $x$, 根据题意,所列方程正确的是($\qquad$)
A. $1999 x^{2}=1360$
B. $1999\left(1-x^{2}\right)=1360$
C. $1999(1-x)^{2}=1360$
D. $1999(1-2 x)=1360$
如图, 任平面直角坐标系中, 矩形 $A B C O$ 的两边与坐标轴重合, $O A=2, O C=1$. 将矩形$ABCO$绕点$O$逆时针旋转，每次旋转$90^{\circ}$，则第$2023$次旋转结束时，点$B$的坐标是($\qquad$)

A. $(-2,-1)$
B. $(-1,2)$
C. $(-2,1)$
D. $(1,-2)$
在二次函数 $y=-x^{2}+2 x$ 中, 若函数值大于 0 , 则结合函数图象判断 $x$ 的取值范围是($\qquad$)
A. $x<0$ 或 $x>2$
B. $x>0$ 或 $x<-2$
C. $-2<x<0$
D. $0<x<2$
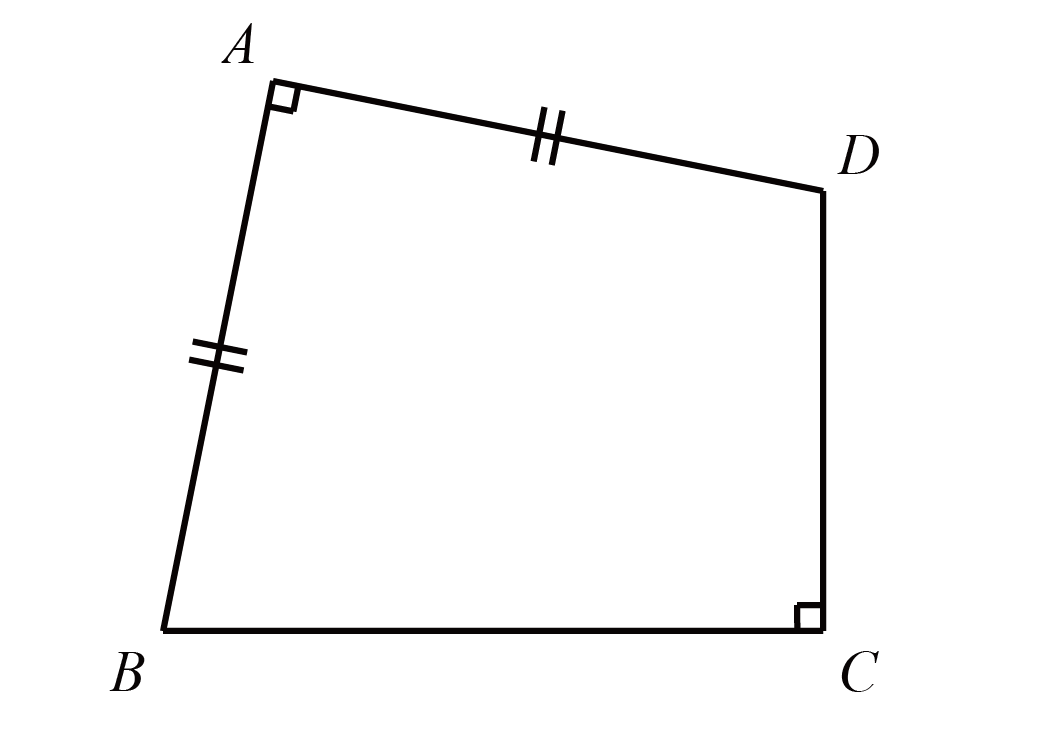
如图, 在圆内接四边形 $A B C D$ 中, $A B=A D$, $\angle B A D=90^{\circ}$. 若四边形 $A B C D$ 的面积是 $S$, $A C$ 的长是 $x$, 则 $S$ 与 $x$ 之间囦数关系式是($\qquad$)

A. $S=x^{2}$
B. $S=\dfrac{1}{2} x^{2}$
C. $S=\sqrt{2} x^{2}$
D. $S=\dfrac{2}{3} x^{2}$
根据频率估计概率原理，可以用随机模拟的方法对圆周率$\pi$进行估计．用计算机随机产生 $m$ 个有序数对 $(x, y)(0 \leqslant x \leqslant 1,0 \leqslant y \leqslant 1)$, 它们对应的点全部在平面直角坐标系中某一个正方形的边界及其内部. 若统计出这些点中到原点的距离小于或等于 1 的点有 $n$ 个, 则可估计 $\pi$ 的值是($\qquad$)
A. $\dfrac{m}{n}$
B. $\dfrac{n}{m}$
C. $\dfrac{2 n}{m}$
D. $\dfrac{4 n}{m}$

第II 卷 (非选择题共 90 分)

二、填空题(共 6 小题，每小题 3 分，共18 分)

下列各题不需要写出解答过程，请将结果直接填写在答题卡指定的位置．
11. 在平面直角坐标系中,点 $P(-3,4)$ 关于原点对标的点的坐标是$\underline{\hspace{3em}}$．

若一个长方形的长比宽多 2 , 且面积为 80 , 则宽是$\underline{\hspace{3em}}$．
如图, $\odot O$ 是 $\triangle A B C$ 的内切圆, $\angle C=40^{\circ}$, 则 $\angle A O B$ 的大小是$\underline{\hspace{3em}}$．
甲、乙、丙三位同学把自己的数学课本放在一起、每人从中随机抽取一本 (不放回)，三位同学抽到的课本都是自己课本的概率是$\underline{\hspace{3em}}$．
已知抛物线 $y=a x^{2}+b x+c(a, b, c)$ 是常数, $\left.0<a<c\right)$ 经过点 $(-1,0)$, 下列结论:
(1) $b>0$;
(2)关于$x$的一元二次方程$ax^2+bx+c=0$有两个不相等的实数根；
(3)当 $x<-1$ 时 $y$ 随 $x$ 的增大而减小;
(4) $m$ 为任意实数, 若 $c=3 a$, 则代数式 $a m^{2}+b m+c$ 的最小值是 $-a$.
其中正确的是$\underline{\hspace{3em}}$ (填写序号).
如图, $D$ 是 $\triangle A B C$ 内一点, $\angle B D C=90^{\circ}, B D=C D, A B=20, A C=21, A D=\dfrac{13 \sqrt{2}}{2}$, 则 $B C$ 的长是$\underline{\hspace{3em}}$．

三、解答题 (共8 小题，共 72 分)

下列各题需要在答题卡指定的位置写出文字说明、证明过程、演算步骤或画出图形.

(本小题满分 8 分)
关于 $x$ 的一元二次方程 $x^{2}+b x+8=0$ 有一个根是 $x=2$, 求 $b$ 的值及方程的另一个根.
(本小题满分 8 分)
如图, 在 $\triangle A B C$ 中, $A C=B C$, 将 $\triangle A B C$ 绕点 $A$ 逆时针旋转 $60^{\circ}$, 得到 $\triangle A D E$, 连接 $B D, B E$.

(1)判断 $\triangle A B D$ 的形状;
(2) 求证: $B E$ 平分 $\angle A B D$.
(本小题满分 8 分)
一个不透明的布袋中装有 1 个红球, 1 个黑球和若干个白球, 它们除颜色外其余都相同. 从中任意摸出 1 个球, 是白球的概率为 $\dfrac{1}{2}$.
（1）直接写出布袋中白球的个数;
（2）从布袋中先摸出一个球后放回, 再摸出一个球, 请用列表或画树状图法求两次摸到的球都是白球的概率.
(本小题渵分 8 分)
如图, $A B, C D$ 是 $\odot O$ 的两条弦, $\angle A O B+\angle C O D=180^{\circ}$.

(1) 在图(1) 中, $\angle A O B=120^{\circ}, C D=6$, 直接写出图中阴影部分的面积;
(2) 在图 (2) 中, $E$ 是 $A B$ 的中点, 判断 $O E$ 与 $C D$ 的数量关系,非证明你的结论.
(本小题满分 8 分)
如图是由小正方形组成的 $7 \times 6$ 网格, 位个小正方形的顶点叫做格点. 仅用无刻度的直尺在给定网格中完成画图.

(1) 在图(1) 中, $A, B, C$ 三点是格点, 画经过这三点的圆的圆心 $O$, 并在该圆上画点 $D$, 使 $\overparen{A D}=\overparen{B C}$;
(2) 在图 (2) 中, $A, E, F$ 三点是格点, $\odot I$ 经过点 $A$. 先过点 $F$ 画 $A E$ 的平行线交 $\odot I$ 于 $M, N$ 两点, 再画弦 $M N$ 的中点 $G$.
(本小题满分 10 分))
燃放畑花是一种常见的喜庆活动. 如图, 小杰燃放一种手持烟花, 这种烟花每隔 $2 \mathrm{~s}$ 发射一枚花弹,每枚花弹的飞行路径视为同一条抛物线,飞行相同时间后发生爆炸. 小杰发射出的第一枚花弹的飞行高度 $h$ (单位:m) 还飞行时间 $t$ (单位:s)变化的规律如下表:

飞行时间t/s 0 0.5 1 4.5 $\cdots$

飞行高度h/m 2 9.5 16 33.5 $\cdots$

(1) 求第一枚花弹的飞行高度 $h$ 与飞行时间 $t$ 的函数解析式 (不要求写出自变量的取值范围）;
(2)当第一枚花弹到达最高点时，求第二枚花弹到达的高度;
(3)为了安全,要求花弹爆炸时的高度不低于 $30 \mathrm{~m}$. 小杰发现在第一枚花弹爆炸的同时,第二枚花弹与它处于同一高度, 请分析花弹的爆炸高度是否符合安全要求.
(本小题满分 10 分)
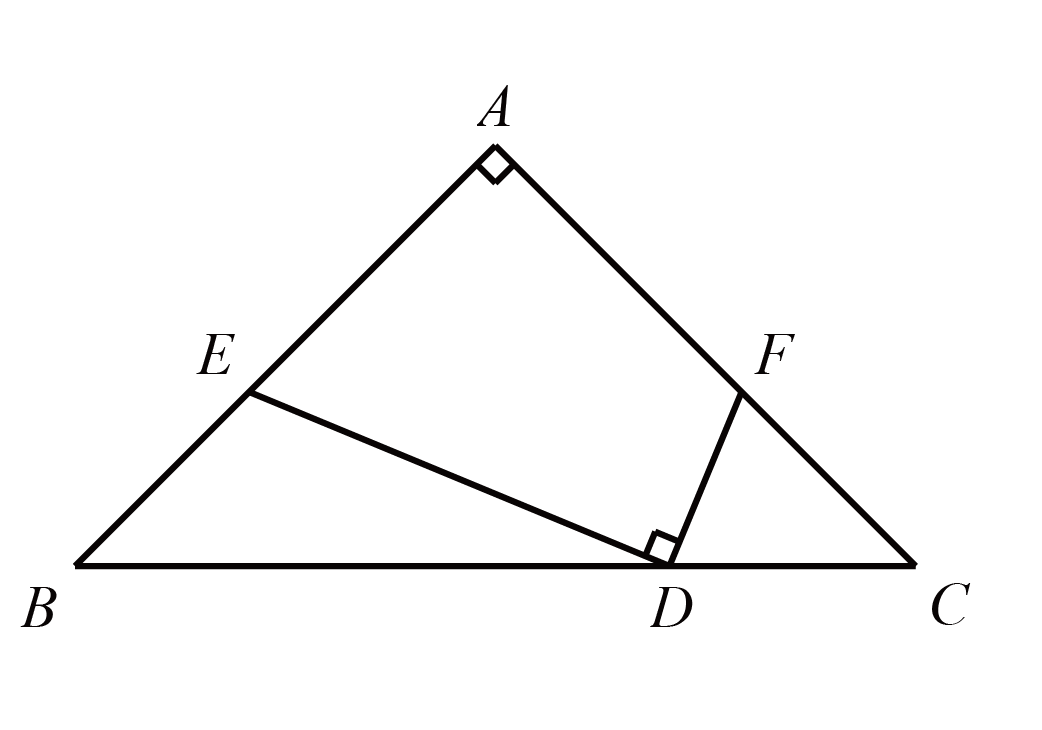
操作与思考 如图 (1), 在 $\triangle A B C$ 中, $A B=A C, \angle B A C=\alpha, D$ 是异于 $A, B$ 的一点, 且. $\angle A D B=90^{\circ}$. 将线段 $A D$ 绕点 $A$ 逆时针旋转 $\alpha$, 画出对应线段 $A E$, 连接 $D E$ 交 $B C$ 于点 $F$, 猜想 $B F$ 与 $C F$ 的数量关系,并证明你的猜想;
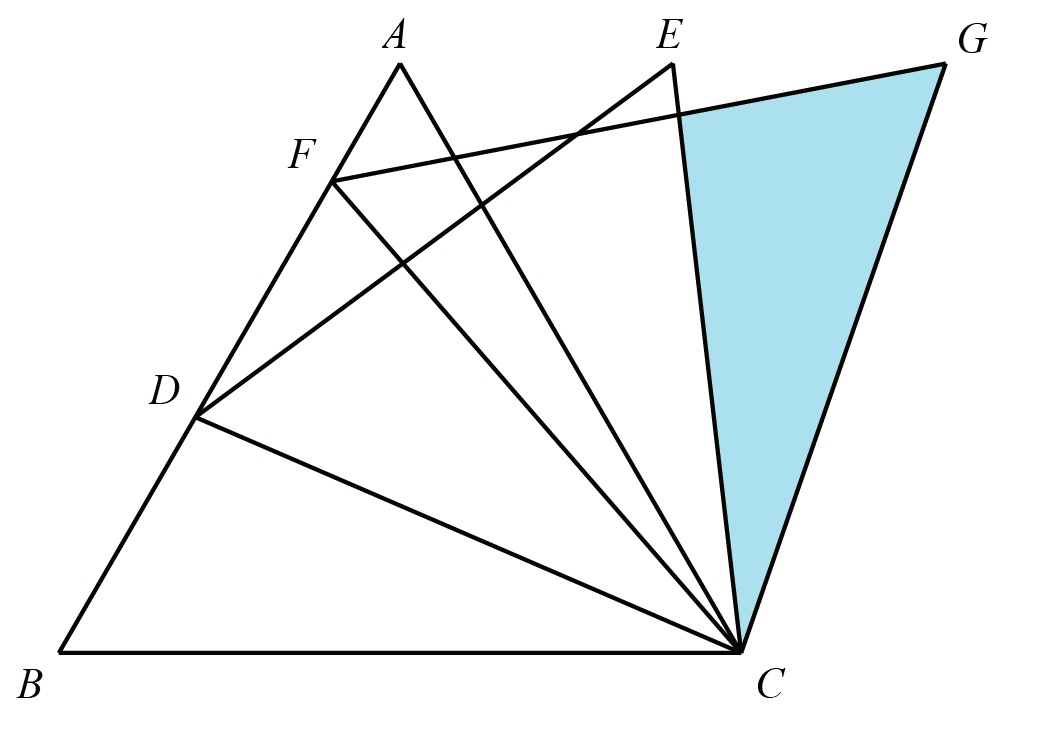
迁移与运用 如图 (2), 在 $\triangle A B C$ 和 $\triangle C D E$ 中, $A C=B C, C D=C E, \angle A C B=\angle D C E=90^{\circ}$, $A C=\sqrt{10}, C D=\sqrt{2}, E D$ 的延长线交 $A B$ 于点 $F$, 且 $\angle B D C=90^{\circ}$, 直接写出 $E F$ 的长.
(本题渵分 12 分)
如图,抛物线 $y=x^{2}-2 x-6$ 与 $x$ 轴分别相交于 $A, B$ 两点 (点 $A$ 在点 $B$ 的左侧), $C$ 是 $A B$ 的中点, 平行四边形 $C D E F$ 的顶点 $D, E$ 均在抛物线上.

(1) 直接写出点 $C$ 的坐标;
(2) 如图 (1), 若点 $D$ 的横坐标是 $-2$, 点 $E$ 在第三象限, 平行四边形 $C D E F$ 的面积是 13 , 求点 $F$ 的坐标;
(3) 如图 (2), 若点 $F$ 在抛物线上, 连接 $D F$, 求证:直线 $D F$ 过一定点.