【初数】问题4 费马点求长度

问题

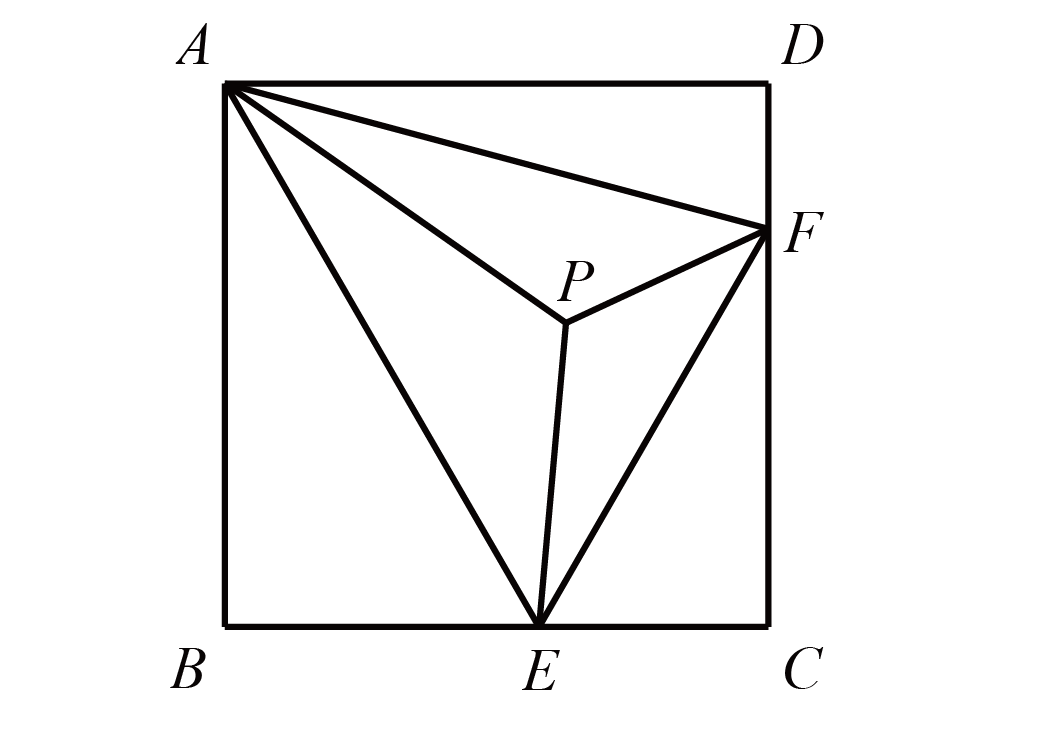
(2021·七一华源) 如图, 在正方形 $A B C D$ 中, $E$, $F$ 分别是边 $B C$, $C D$ 上的一点, $E F=B E+D F$, 在 $\triangle A E F$ 内部有一点 $P$, 且 $\angle A P E=\angle A P F=120^{\circ}$, $P A=2 \sqrt{3}+2$, $P E=4$, 则 $P F^{2}=\underline{\hspace{3em}}$

解答

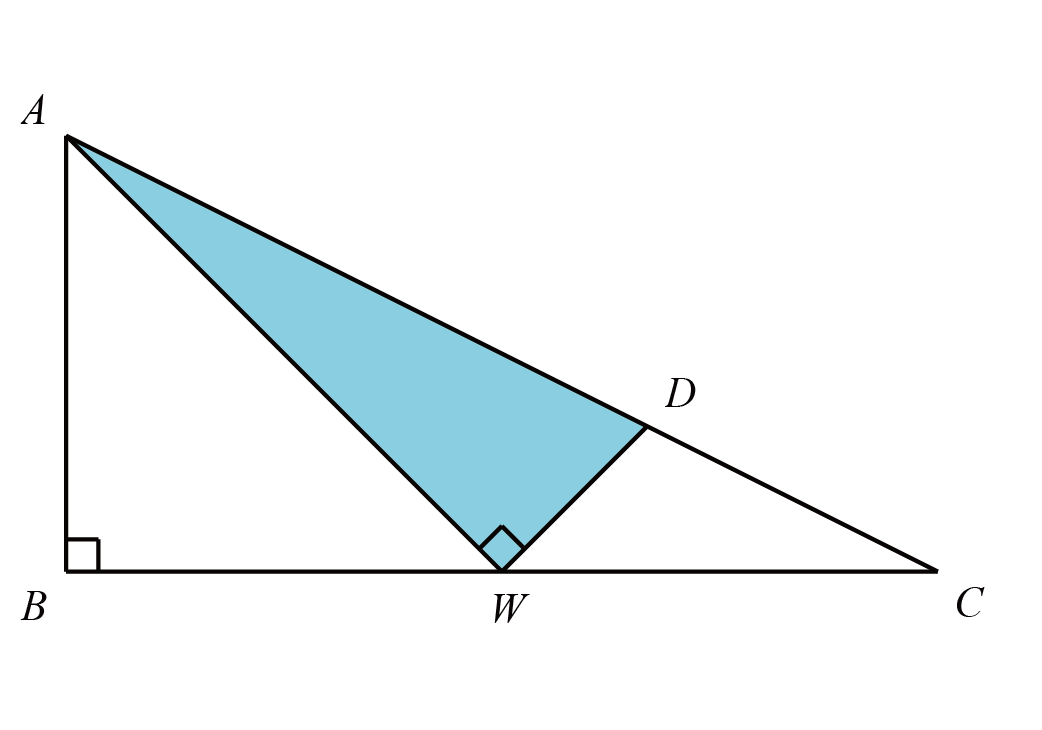
如图，以$PA$为边构造正$\triangle PAW$，连接$WE$，过$E$作$EX \bot PW$于$X$

则$PW=PA=2\sqrt{3}+2$，$\angle EPX=60^{\circ}$

所以$$PX=\dfrac{1}{2}PE=2$$

$$EX=\sqrt{PE^2-PX^2}=\sqrt{4^2-2^2}=2\sqrt{3}$$

所以$$WX=PW-PX=2\sqrt{3}=EX$$

故$\triangle WXE$是等腰直角三角形，从而$\angle EWF=45^{\circ}$

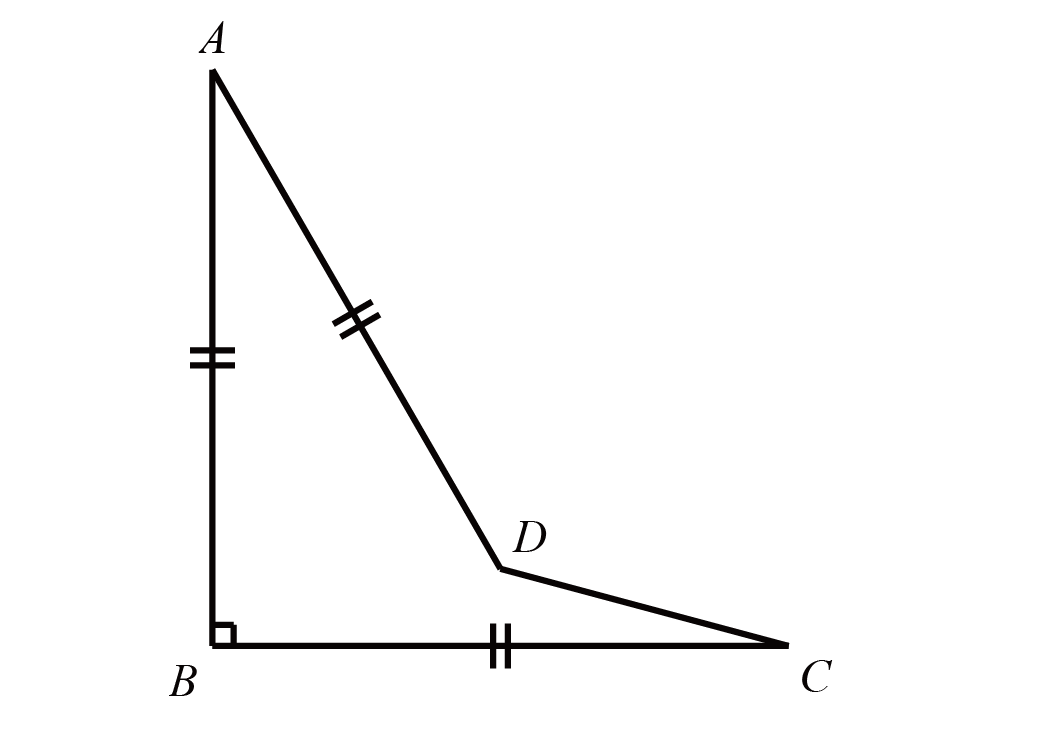
又因为$EF=BE+DF$，根据夹半角模型可得$\angle EAF=45^{\circ}$

所以$$\angle EAF=\angle FWE$$

因此$A$、$W$、$E$、$F$四点共圆，那么$\angle AEF=\angle AWF=60^{\circ}$

又因为$$\angle PAE+\angle AEP=\angle AEP+\angle PEF=60^{\circ}$$

所以$\angle PAE=\angle PEF$，又$\angle APE=\angle EPF=120^{\circ}$

所以$$\triangle PAE \sim \triangle PEF$$

那么$$\dfrac{PA}{PE}=\dfrac{PE}{PF}$$

从而$$PF=\dfrac{PE^2}{PA}=\dfrac{4^2}{2\sqrt{3}+2}=4\sqrt{3}-4$$

因此$PF^2=(4\sqrt{3}-4)^2=64-32\sqrt{3}$