【初数】问题3 夹半角求长度

问题

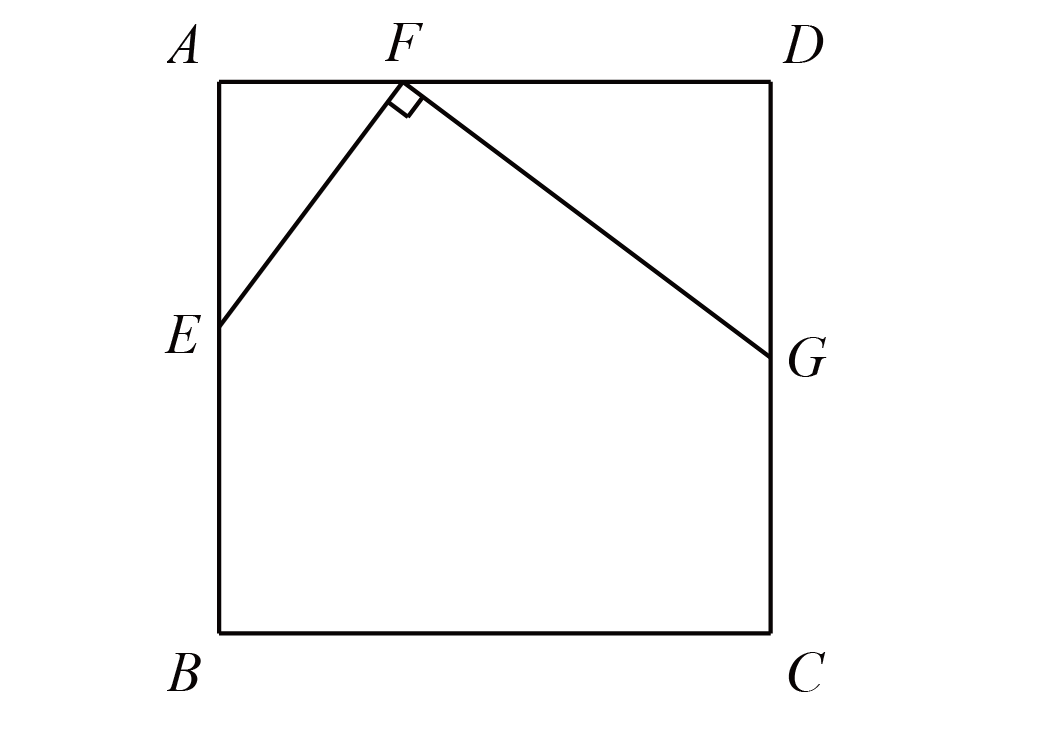
(2021·武汉一初) 如图, 正方形 $A B C D$ 中, 点 $E$, $F$ 分别是边 $A B$, $A D$ 上一点, 且 $B E=E F$, 过 $F$ 点作 $E F$ 的垂线交 $C D$ 边与 $G$ 点, 已知 $A F=1, F G=\dfrac{5}{2}$, 则 $A B=\underline{\hspace{3em}}$.

解答

如图，过$B$作$BP \bot FG$于$P$，连接$BF$、$BG$，则$EF// BP$

因为$BE=EF$，所以$\angle EBF=\angle EFB=\angle FBP$

又因为$\angle BAF=\angle BPF=90^{\circ}$，$BF=BF$

故$$\triangle BFA \cong \triangle BPF$$

所以$PF=AF=1$，$BP=BA=BC$

所以$$\text{Rt} \triangle BGP \cong \text{Rt} \triangle BGC$$

所以$GC=GP=FG-AF=\dfrac{5}{2}-1=\dfrac{3}{2}$

设正方形边长为$x$，则$DF=x-1$，$DG=x-\dfrac{3}{2}$，$FG=\dfrac{5}{2}$

根据勾股定理：$DF^2+DG^2=FG^2$

所以$$(x-1)^2+(x-\dfrac{3}{2})^2=\left(\dfrac{5}{2}\right)^2$$

化简得$$(x-3)(2x+1)=0$$

解得$x=3$或$x=-\dfrac{1}{2}$（舍），故$AB=3$。