【小奥】问题6 梯形求线段比

问题

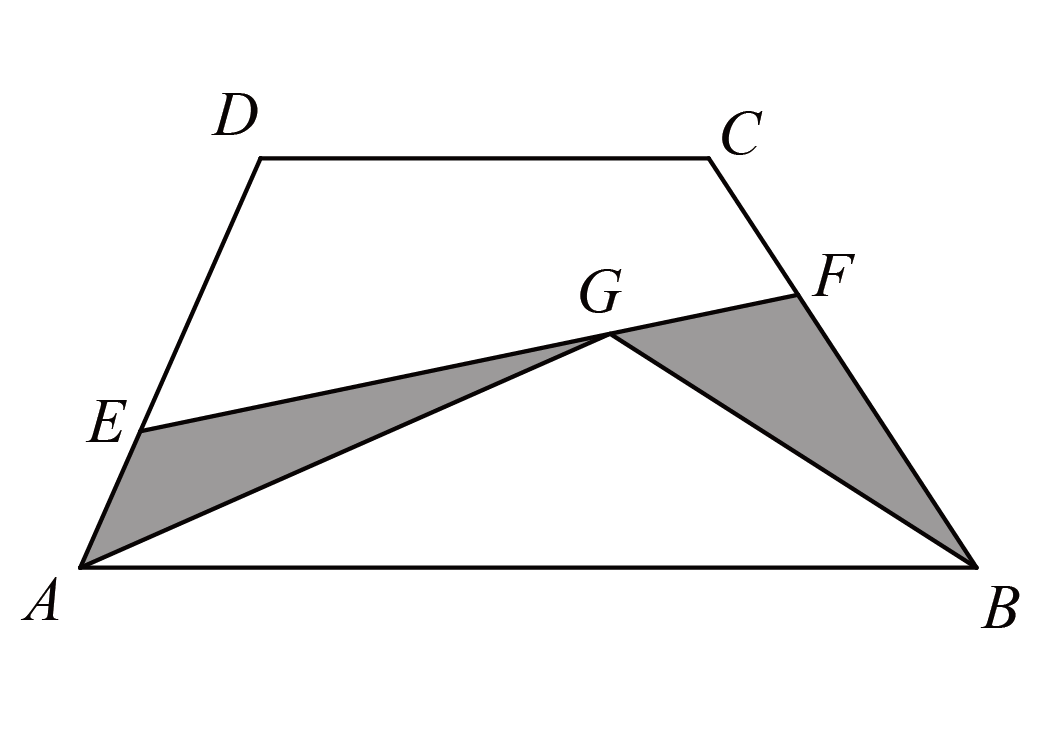
如图，梯形$ABCD$中，$AB=2CD$，$DE=2EA$，$BF=2FC$，连接$EF$，$G$为$EF$上一点，图中两块阴影部分的面积相等，求$EG:GF$．

解析

如图，延长$AD$和$BC$交于点$H$，连接$GD$、$GH$、$GC$，因为$AB$和$CD$平行，则

$$HD:HA=HC:HB=CD:AB=1:2$$

所以$AD=DH$，$BC=CH$，设$S_{\triangle AEG}=S_{\triangle BFG}=2a$

则$$S_{\triangle DEG}=4a，S_{\triangle DHG}=6a$$

$$S_{\triangle GFC}=a，S_{\triangle CHG}=3a$$

所以

$$EG:GF=S_{\triangle EGH}:S_{\triangle FGH}=10a:4a=5:2$$