【小奥】问题7 等腰直求面积

问题

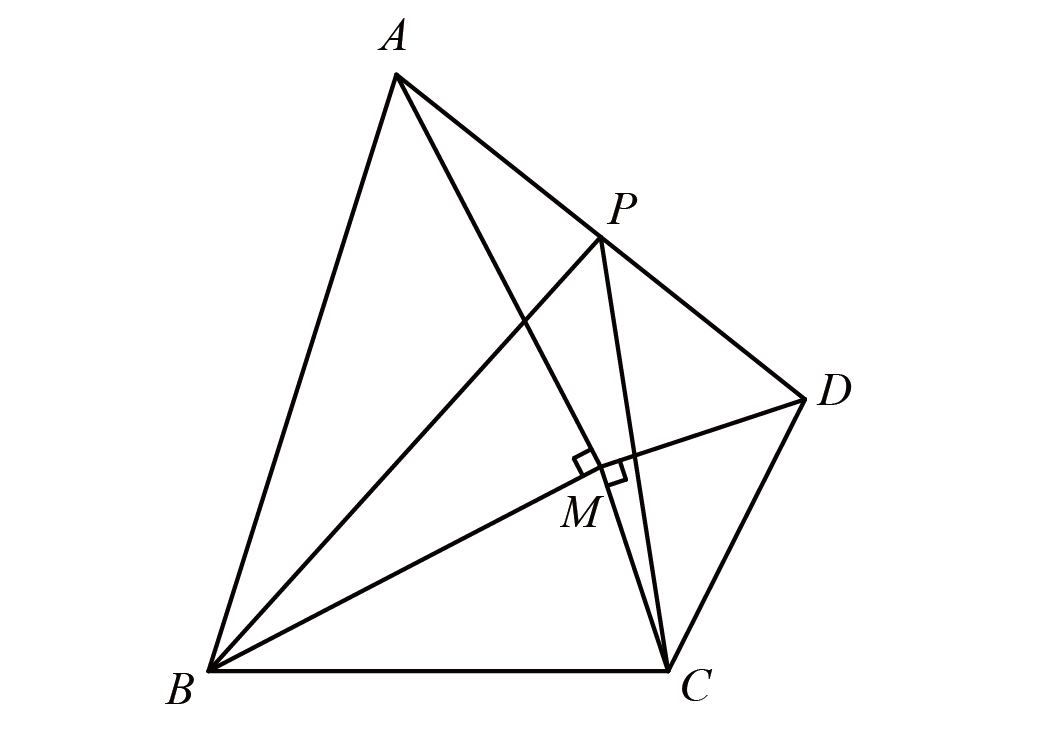
四边形$ABCD$内有一点$M$使得$\triangle ABM$、$\triangle CDM$均为等腰直角三角形，$P$为$AD$的中点，已知$BC=18$，三角形$BCM$中$BC$边上的高为$8$，求$\triangle PBC$的面积．

法1：旋转

将三角形$ADM$顺时针旋转$90{}^\circ $得$\triangle { {A}^{\prime } }CM$，易知$PM$垂直于${ {P}^{\prime } }M$，且${ {P}^{\prime } }M$为三角形${ {A}^{\prime } }BC$的中位线，可知

$${ {P}^{\prime } }M=BC\div 2=9$$

由于$PM$垂直于${ {P}^{\prime } }M$，所以$PM$也垂直$BC$，可知三角形$PBC$的面积为

$$18\times \left( 9+8 \right)\div 2=153$$

法2：弦图

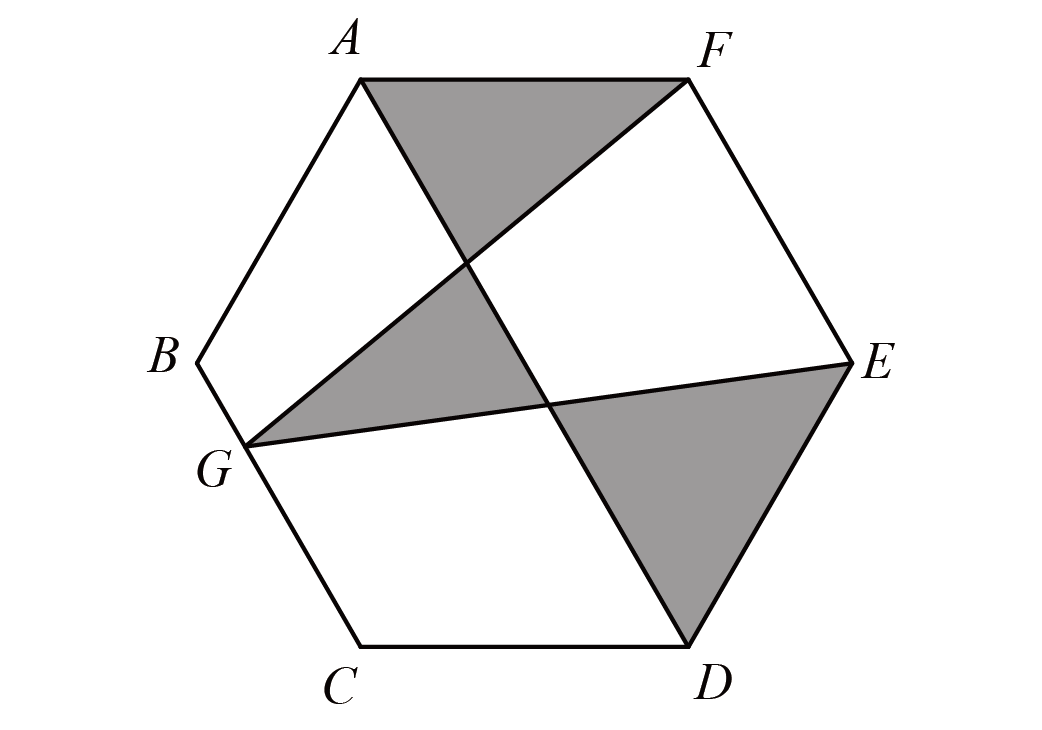
如图，构造弦图，易得$MG=BI$，$HM=IC$，所以

$$\begin{aligned}
GI+HI&=MG+MI+HM+MI& \\
&=BI+IC+2MI \\
&=BC+2MI \\
&=18+2\times 8 \\
&=34
\end{aligned}$$

而$$S_{\triangle ABC}=\frac{1}{2}\times BC\times GI$$

$$S_{\triangle DBC}=\frac{1}{2}\times BC\times HI$$

那么

$$\begin{aligned}
S_{\triangle ABC}+S_{\triangle DBC}&=\frac{1}{2}\times BC\times(GI+HI) \\
&=\dfrac{1}{2}\times18\times  (18+16) \\
&=306
\end{aligned}$$

因此$$S_{\triangle PBC}=\frac{1}{2}(S_{\triangle ABC}+S_{\triangle DBC})=153$$

法3：倍长中线

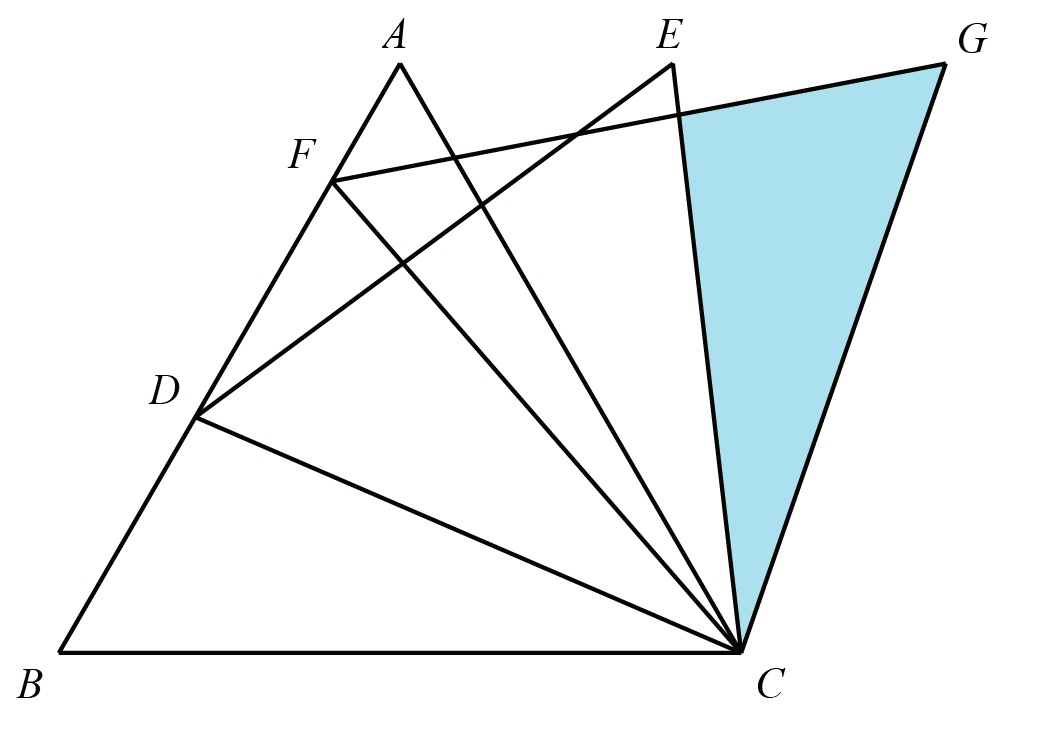
如图，连接$MP$并延长至$M^{\prime}$，使得$PM^{\prime}=PM$，连接$DM^{\prime}$，易得

$$\triangle MPA \cong \triangle M^{\prime}PD$$

所以$MA=M^{\prime}D$，故$BM=M^{\prime}D$，$CM=MD$，$\angle BMC=M^{‘}DM$，所以

$$\triangle BMC \cong \triangle M^{\prime}DM$$

故$PM=\dfrac{1}{2}MM^{\prime}=\dfrac{1}{2}BC=9$，且$PM$和$BC$垂直，那么

$$S_{\triangle PBC}=\frac{1}{2}\times 18 \times (9+8)=153$$