【小奥】问题8 四块三角形面积相等

问题

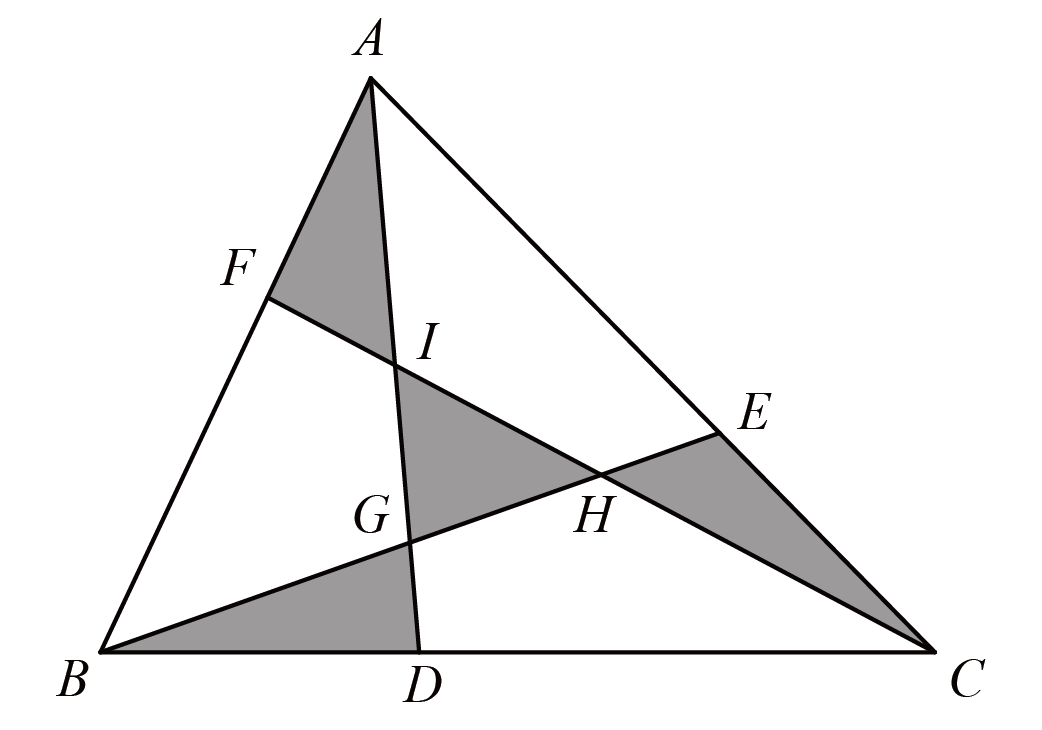
如图，$4$个阴影三角形的面积相等，已知$AE:EC=a:1$，求$a-\dfrac{1}{a}$．

解析

如图，连接$AH$、$FG$、$CG$、$IE$，设$BF:FA=b:1$，$CD:DB=c:1$，因为

$$S_{\triangle AFI}=S_{\triangle GHI}$$

所以

$$S_{\triangle AFH}=S_{\triangle AGH}$$

从而$FG$和$AH$平行，同理$IE$和$GC$平行，那么

$$BF:BA=FG:AH=GI:IA=CE:EA=1:a$$

即

$$\dfrac{b}{b+1}=\dfrac{1}{a}$$

那么

$$a=1+\dfrac{1}{b}$$

同理可得$b=1+\dfrac{1}{c}$，$c=1+\dfrac{1}{a}$

因此

$$a=1+\dfrac{1}{1+\dfrac{1}{c}}=1+\dfrac{c}{c+1}=1+\dfrac{1+\dfrac{1}{a}}{2+\dfrac{1}{a}}$$

整理可得$a^2=a+1$，那么$a-\dfrac{1}{a}=\dfrac{a^2-1}{a}=\dfrac{a}{a}=1$．