2026年“数学花园探秘”科普活动小学高年级组决赛试卷 A-邱福星的教学页面

一、填空题（每小题$ 8 $分，共$ 32 $分）

算式$ 20 \times (26^2 – 13^2) \div \dfrac{4^2 – 3^2}{\dfrac{1}{3+\dfrac{1}{4}} + \dfrac{1}{\dfrac{1}{3}+4}} $的计算结果是$ \underline{\quad \quad} $。

$780$
原式$ = 20 \times (26+13) \times (26-13) \div \dfrac{16-9}{\dfrac{4}{3 \times 4 + 1} + \dfrac{3}{1 + 4 \times 3}}$
$= 20 \times 39 \times 13 \div \dfrac{7 \times 13}{7}$
$= 780$

在下面的除法竖式中每个方框内填上合适的数字，使得竖式成立。那么竖式中的商是$\underline{\quad \quad} $。

$199$
$(1) $由第四、五行，得$ 102\square$、$9\square6$；
(2) 第三行，得$ 10\square$，进而除数是$ 10\square$；
(3) 商的百位为$1$，十位为$9$，进而除数是$ 104$；
(4) 结合第四、五、六行，得商为$ 199$；

如图，在边长为$ 100 $的正十二边形中，分别以顶点$ A$、$B$、$C$、$D$、$E$、$F $为圆心，以正十二边形边长为半径画圆。那么图中阴影部分的周长是$\underline{\quad \quad} $。（$\pi $取$ 3.14$）

$942$
分别连接$ AL$、$AG$、$BL$、$FG$，

(1) 正十二边形每个内角：$(12-2) \times 180^{\circ} \div 12 = 150^{\circ}$；
(2) 由已知，$AG=GF=FA=AA$，$ AB_1=B_1B=BL=LA$，
所以$ \angle A_1AG = \angle B_1AL = 30^{\circ}$，
所以$ \angle GAL = 150^{\circ} – \angle A_1AG – \angle B_1AL = 90^{\circ}$；
(3) 阴影部分为$ 6 $个内角为$ 90^{\circ}$，半径为$ 100 $的圆弧的和：
$C = \dfrac{6 \times 90^{\circ}}{360^{\circ}} \times 2\pi \times 100 = 300\pi = 942$；

甲、乙两个工程队合作完成某项任务。如果先由甲队人数的$ \dfrac{1}{9} $和乙队人数的$ \dfrac{1}{12} $一起工作$ 3 $天，再由甲队人数的$ \dfrac{1}{8} $和乙队人数的$ \dfrac{1}{6} $一起工作$ 2 $天，恰好共完成全部任务的$ \dfrac{1}{60}$。如果最开始甲、乙两队全部人员一起同时工作，那么需要$\underline{\quad \quad} $天能完成任务。

$35$
相当于甲队的$ \dfrac{1}{9} \times 3 + \dfrac{1}{8} \times 2 = \dfrac{7}{12} $和乙队的$ \dfrac{1}{12} \times 3 + \dfrac{1}{6} \times 2 = \dfrac{7}{12} $一起工作$ 1 $天完成全部任务的$ \dfrac{1}{60}$。
因此甲、乙全部人员一起工作，需要$ \dfrac{7}{12} \div \dfrac{1}{60} = 35 $天。

二、填空题（每小题$ 10 $分，共$ 40 $分）

末三位数字相同且能被$ 2026 $整除的五位数是$\underline{\quad \quad} $。

$95222$
设五位数是$ 2026 \times \overline{ab} = \overline{ABCCC}$，$A$、$B$、$C $可能相同，$a $可能为$ 0$，
其中$ C $可能是$ 0$、$2$、$4$、$6$、$8$，
因为$ 2026 $的百位为$ 0$，
所以$ 2026 \times \overline{ab} \equiv 26 \times \overline{ab} \pmod{1000}$（即$ 26 \times \overline{ab} $决定$ 2026 \times \overline{ab} $的末三位），
因为$ 99999 \div 2026 = 49 \dots 725$，$ 26 \times 49 = 1274$，$ 26 \times 2 \times 13$，
只可能是$ 26 \times \overline{ab} = 1222$（$\overline{CCC} $不是$ 13 $的倍数），
所以$ \overline{ab} = 47$，即$ 2026 \times 47 = 95222$；

算式$ 357 \times \left( \dfrac{1}{2 \times 5} + \dfrac{1}{3 \times 8} + \dfrac{1}{5 \times 13} + \dfrac{1}{8 \times 21} + \dfrac{1}{13 \times 34} \right) $的计算结果是$\underline{\quad \quad} $。

$59$
原式$ = 357 \times \left( \dfrac{1}{3} \times \dfrac{3}{2 \times 5} + \dfrac{1}{5} \times \dfrac{5}{3 \times 8} + \dfrac{1}{8} \times \dfrac{8}{5 \times 13} + \dfrac{1}{13} \times \dfrac{13}{8 \times 21} + \dfrac{1}{21} \times \dfrac{21}{13 \times 34} \right)$
$= 357 \times \left[ \dfrac{1}{3} \times \left( \dfrac{1}{2} – \dfrac{1}{5} \right) + \dfrac{1}{5} \times \left( \dfrac{1}{3} – \dfrac{1}{8} \right) + \dfrac{1}{8} \times \left( \dfrac{1}{5} – \dfrac{1}{13} \right) + \dfrac{1}{13} \times \left( \dfrac{1}{8} – \dfrac{1}{21} \right) + \dfrac{1}{21} \times \left( \dfrac{1}{13} – \dfrac{1}{34} \right) \right]$
$= 357 \times \left( \dfrac{1}{2 \times 3} – \dfrac{1}{3 \times 5} + \dfrac{1}{3 \times 5} – \dfrac{1}{5 \times 8} + \dfrac{1}{5 \times 8} – \dfrac{1}{8 \times 13} + \dfrac{1}{8 \times 13} – \dfrac{1}{13 \times 21} + \dfrac{1}{13 \times 21} – \dfrac{1}{21 \times 34} \right)$
$= 357 \times \left( \dfrac{1}{2 \times 3} – \dfrac{1}{21 \times 34} \right)$
$= 357 \times \dfrac{1}{6} \times \left( 1 – \dfrac{1}{7 \times 17} \right)$
$= 59$

如图所示，用$ 7 $个相同的长方形摆出一个“房子”。已知“房子”的高度是$ 122$，那么一个小长方形的面积是$\underline{\quad \quad} $。

$400$
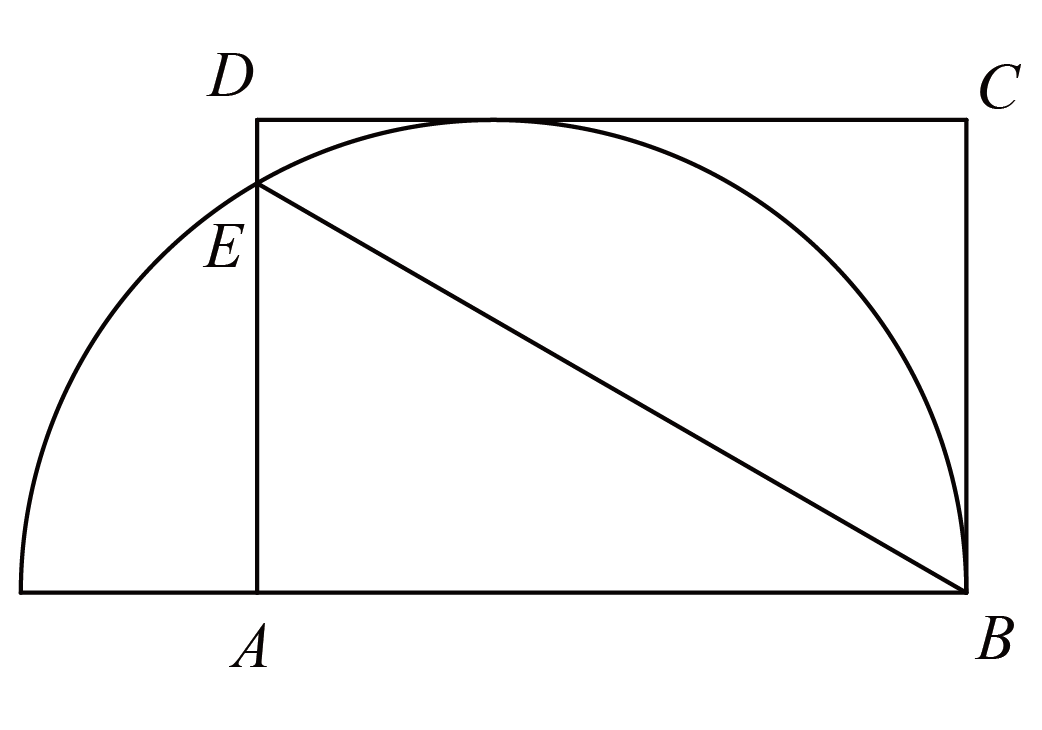
如图，分别过点$ A$、$C $作$ EF $的垂线分别交$ EF $于点$ B$、$D$，

设长方形的长为$ a$，宽为$ b$，则$ EF = a+b$，$ FC = A$，$ CE = a-b$，
(1) 在直角三角形$ FCE $中，$\angle FCE = 90^{\circ}$，由勾股定理得，
$FC^2 + CE^2 = FE^2$，即$ a^2 + (a-b)^2 = (a+b)^2$，
所以$ a^2 = (a+b)^2 – (a-b)^2$，即$ a^2 = 2a \times 2b$，
所以$ a = 4b$；
(2) 在直角三角形$ FCE $中，$S_{\triangle FCE} = \dfrac{1}{2} FC \times CE = \dfrac{1}{2} FE \times CD$，
所以$ a \times (a-b) = (a+b) \times CD$，即$ CD = 2.4b$；
(3) 因为$ AB$、$CD $分别与$ EF $垂直，
所以$ AB // CD$，
所以$ \dfrac{AB}{CD} = \dfrac{AE}{CE}$，即$ \dfrac{AB}{2.4b} = \dfrac{a}{a-b}$，
所以$ AB = 3.2b$；
(4) 因此，$ 122 = a + 3.2b + b + a$，即$ b=10$，
所以一个小长方形的面积：$ a \times b = (4 \times 10) \times 10 = 400$；

老师写了五个连续的两位数，将其中的三个分别给了甲、乙、丙三位同学，三位同学只知道自己拿到的数，而不知道其他同学拿到的数。他们依次对话如下：
师：“我写的这五个书的和，是一个平方数。”
甲：“另外两位同学拿到的一定有偶数。”
乙：“另外两位同学拿到的一定互质。”
丙：“乙拿到的数的奇数个因数。”
如果他们都聪明且诚实，那么丙拿到的数是$\underline{\quad \quad} $。

$78$
由老师的话可得，$5$个连续的两位数的和为$ 5 \times $中间数，结果是一个平方数，
因此中间数为$ 5 \times k^2$，$k $可以取$ 2$、$3$、$4$，得到五个数的情况有$ 3 $种：
(1) $18$，$ 19$，$ 20$，$ 21$，$ 22$;
(2) $43$，$ 44$，$ 45$，$ 46$，$ 47$;
(3) $78$，$ 79$，$ 80$，$ 81$，$ 82$;
由甲的话可得，五个数为$ 2 $奇$ 3 $偶，甲拿到的是奇数；则乙、丙中必有偶数，
因此只能是情况 (1) 或情况 (3)；
由乙的话可得，乙在情况 (1) 拿到$ 18 $或$ 21$，在情况 (3) 中拿到$ 78 $或$ 81$；
由丙的话可得，乙拿到$ 81$，丙能知道乙拿到的是$ 81 $而不是$ 78$，
只能是丙拿到了$ 78$；

三、填空题$ III$（每小题$ 14 $分，共$ 42 $分）

甲、乙两人分别从$ A$、$B $两地出发，相向而行。甲先出发，$30 $分钟后乙出发，$15 $分钟后两人在两地中点$ C $处相遇。若两人出发时间不变，但出发时甲的速度增加$ 5 $米$/$分，乙的速度增加$ 60 $米$/$分，那么两人仍然会在$ C $点相遇，那么$ AB $两地相距$\underline{\quad \quad} $米。

$3600$
过程$1$：甲走$ 30+15=45 $分钟、乙走$ 15 $分钟，各自走$ AB $的一半，
因此$ v_{\text{$甲$}} : v_{\text{$乙$}} = 1:3$；
过程$2$：甲、乙各自速度增加后，按过程$ 1 $的时间行走，
（当在$ C $点相遇时，两人继续走，此时时间相同，路程与速度成反比）
甲比过程$ 1 $多走$ 5 \times 45 = 225 $米，乙比过程$ 1 $多走$ 60 \times 15 = 900 $米，

因此 $v^\prime_{\text{甲}} : v^\prime_{\text{乙}} = 225:900 = 1:4$；
由$ v_{\text{甲}} : v_{\text{乙}} = 1:3$，当甲的速度增加$ 5 $米$/$分，乙的速度增加$ 15 $米$/$分，
则甲、乙速度比仍为$ 1:3$，
由 $v^\prime_{\text{甲}} : v^\prime_{\text{乙}} = 1:4$，与$ 1:3 $对比，乙速度增加多$ 1 $份，而实际增加$ 60-15=45 $米$/$分，
所以 $v^\prime_{\text{甲}} = 45 $米$/$分，即甲原来速度是$ 45-5=40 $米$/$分，
那么$ AB $两地相距：$ 40 \times 45 \times 2 = 3600 $米；

如图，最左边的方格中有一枚棋子，其余方格依次编号为$ 1$~$26$，每次只可以向右将棋子移动到最近的编号为$ 2 $或$ 5 $的倍数的方格。例如：第一次只能将棋子移动到$ 2 $号或$ 5 $号的方格中；如果棋子在$ 8 $号方格，只能移动到$ 10 $号方格；如果棋子在$ 15 $号方格，只能移动到$ 16 $号或$ 20 $号方格。那么将棋子移动到$ 26 $号方格共有$\underline{\quad \quad} $种移动方法。

$484$
由已知，可标数如下：

如图，圆周上写有$ 5 $个$ 0 $和$ 1 $个正整数$ A$，每次进行如下操作：选定某个圆圈，将圆圈中的数减$ 1$，同时将相邻两个圆圈中的数各加$ 3$。如果若干次操作后能将$ 6 $个数都变为$ 2026$，那么$ A $的最小值是$\underline{\quad \quad} $。

$56$
如图编号，$A $为$ A_1$，顺时针依次为$ B_1$、$A_2$、$B_2$、$A_3$、$B_1$，

若$ A_i $减$ 1$，$B_i $和$ B_j $各加$ 3$，则：
(1) $A_i $与$ B_i $的差除以$ (3+1=4) $的余数相同，
因为若干次操作后$ 6 $个数均为$ 2026$，
所以$ A_i – B_i \equiv 0 \pmod 4$，
所以$ A_i \equiv 0 \pmod 4$；
(2) 每次操作，$6 $个数的总和增加$ (3+3-1=5)$，
因为若干次操作后$ 6 $个数均为$ 2026$，
所以$ A_1 + 5 \times 0 \equiv 6 \times 2026 \equiv 1 \pmod 5$，
所以$ A_1 \equiv 1 \pmod 5$；
(3) $B_1$、$B_2$、$B_3 $的和与$ A_1$、$A_2$、$A_3 $的和作差，
除以$ (3+3+1=7) $的余数相同，
因为若干次操作后$ 6 $个数均为$ 2026$，
所以$ (A_1 + A_2 + A_3) – (B_1 + B_2 + B_3) \equiv 0 \pmod 7$，
所以$ A_1 \equiv 0 \pmod 7$；
$A_1 \equiv 0 \pmod 4$
也就是$ A_1 \equiv 1 \pmod 5$，所以$ A_1 $最小为$ 56$；
$A_1 \equiv 0 \pmod 7$
构造：从$ A $顺时针分别操作次数：$400$，$ 395$，$ 407$，$ 416$，$ 407$，$ 395$；

四、解答题（每小题$ 18 $分，共$ 36 $分，写出详细解答过程）

如图，点$ A$、$B$、$C$、$D $是由边长为$ 10 $的小正方形组成的网格中的四个格点，过形内一点$ G $的三条线段$ AE$、$CF$、$PQ $均平分四边形$ ABCD $的面积。
(1) 四边形$ ABCD $的面积是多少？（$3 $分）
(2) 三角形$ CEG $的面积是多少？（$6 $分）
(3) 三角形$ APQ $的面积是多少？（$9 $分）

$(1) 7200$；$ (2) 900$；$ (3) 3200$
$(1) $连接$ AC$，

在三角形$ ADC $中，$DC = 8 \times 10 = 80$，点$ A $到$ DC $的高$ h_1 = 3 \times 10 = 30$，
所以，$S_{\triangle ADC} = 80 \times 30 \div 2 = 1200$；
在三角形$ ABC $中，$BC = 12 \times 10 = 120$，点$ A $到$ DC $的高$ h_2 = 10 \times 10 = 100$，
所以，$S_{\triangle ABC} = 120 \times 100 \div 2 = 6000$；
所以，$S_{\text{$四边形$}ABCD} = S_{\triangle ADC} + S_{\triangle ABC} = 1200 + 6000 = 7200$；………………………$3$分
【备注：通过补为大长方形减去$ 2 $个小直角三角形、补为直角梯形减去$ 1 $个直角三角形、毕克定理等方法，只要答案正确且有必要过程，给$ 3 $分，仅有答案无过程给$ 1 $分。】
(2) 连接$ EF$，
由 (1) 得$ S_{\triangle ADC} = 1200$，$S_{\text{$四边形$}ABCD} = 7200$，
因为线段$ AE$、$CF $均平分四边形$ ABCD $的面积，
所以$ S_{\text{$四边形$}AECD} = S_{\triangle ABE} = S_{\triangle BCF} = 7200 \div 2 = 3600$，
所以$ EF // AC$，$BE : EC = S_{\triangle ABE} : S_{\triangle AEC} = 3600 : (3600 – 1200) = 3 : 2$；………………………$3$分
所以$ \dfrac{EG}{GA} = \dfrac{EF}{AC} = \dfrac{BE}{BC} = \dfrac{3}{3+2} = \dfrac{3}{5}$，
所以$ S_{\triangle CEG} = \dfrac{3}{5+3} \times S_{\triangle AEC} = \dfrac{3}{8} \times (3600 – 1200) = 900$；………………………$3$分
【备注：通过面积法求出$ BE:EC$、$AF:FB$，但没有求出$ S_{\triangle CEG}$，只给$ 3 $分；通过面积法求出$ EG:GA $或结合三角形$ FEC $求$ FG:GC $或连$ BG $等方法得$ S_{\triangle CEG}$，均可得分。】
(3) 分别连接$ FP$、$QC$，

因为线段$ PQ $均平分四边形$ ABCD $的面积，
所以$ S_{\text{$四边形$}BCPQ} = S_{\triangle BCF}$，即$ S_{\triangle QFG} : S_{\triangle PGC}$，
所以$ FP // QC$，则$ \dfrac{AG}{GE} = \dfrac{CG}{GF} = \dfrac{QG}{GP}$，
分别连接$ AP$、$EP$、$BP$，

所以$ EP // AB$，则$ S_{\triangle ABP} = S_{\triangle ABE} = 3600$，………………………$3$分
所以$ S_{\triangle ADP} + S_{\triangle BPC} = \dfrac{1}{2} \times DP \times 30 + \dfrac{1}{2} \times (80 – DP) \times 120 = 3600$，
解得$ DP = \dfrac{80}{3}$，则$ S_{\triangle ADP} = \dfrac{1}{2} \times \dfrac{80}{3} \times 30 = 400$，………………………$3$分
所以$ S_{\triangle APQ} = 3600 – 400 = 3200$；………………………$3$分
【备注：说明$ EP // AB $得$ 3 $分，求出$ DP $长度或$ DP // PC $的值得$ 3 $分，求出最后结果得$ 3 $分。】

圆周上等距排列着若干枚棋子，每次操作会同时在所有相邻的同色棋子之间放入一枚白棋，在所有相邻的异色棋子之间放入一枚黑棋。例如：

(1) 所给示例如果再操作$ 1 $次，圆周上将共有$\underline{\quad \quad} $枚棋子；（$3 $分，请直接给出答案。）
(2) 所给示例如果再操作$ 2 $次，圆周上将共有$\underline{\quad \quad} $枚棋子；（$6 $分，请直接给出答案。）
(3) 如果开始时如图放置了$ 5 $枚棋子，那么操作$ 9 $次后，圆周上将共有多少枚白棋？（$9 $分）

$(1) 24$;$ (2) 21$;$ (3) 1195$
$(1) n $枚棋子则有$ n $个间隔，
则每次操作后会由$ n $枚棋子变为$ 2n $枚棋子；
那么$ 3 $枚棋子共操作$ 3 $次，共有$ 3 \times 2^3 = 24 $枚棋子；
(2) $1 $黑$ 2 $白，列表如下：

每个棋子各数$ 2 $次，所以黑棋有：$(10 \times 2 + 22 \times 1) \div 2 = 21 $枚；
(3) 两枚相邻的棋子，共$ 3 $种情况：黑黑、黑白、白白，
若相邻是$ 1 $组黑黑，在中间增加$ 1 $枚白棋，则变为$ 2 $组黑白，
若相邻是$ 1 $组黑白，在中间增加$ 1 $枚黑棋，则变为$ 1 $组黑黑、$1 $组黑白，
若相邻是$ 1 $组白白，在中间增加$ 1 $枚白棋，则变为$ 2 $组白白，
设第$ n $次操作后有$ a_n $组黑黑、$b_n $组黑白、$c_n $组白白，$(n $为自然数$)$
则第$ (n+1) $次操作后有：$b_n $组黑黑、$2a_n + b_n $组黑白、$2c_n $组白白，………………………$3$分
$3 $黑$ 2 $白，列表如下：

$……………………………………………………………………………3$分
每个棋子各数$ 2 $次，所以白棋有：$(512 \times 2 + 1366 \times 1) \div 2 = 1195 $枚；………………………$3$分
【备注：第$ (1) (2) $问不需要过程，填出答案直接给分，第 (3) 问，通过纯枚举得出答案，得到全分，中间过程有错但答案对得$ 6 $分；递推说明$ 3 $分、递推过程$ 3 $分、答案$ 3 $分；没有任何过程只有答案得$ 3 $分。】