第34届 WMO 世界奥林匹克 融合创新讨论大会五年级试题

须知：
1. 测评期间，不得使用计算工具或手机。
2. 本卷共$ 120 $分，选择题为单选，每小题$ 5 $分，共$ 80 $分；解答题每小题$ 10 $分，共$ 40 $分。
3. 请将答案写在答题卡上。测评结束时，试卷、答案卡及草稿纸会被收回。
4. 若计算结果是分数，请化至最简。

$($满分$ 120 $分，时间$ 90 $分钟$)$

一、选择题（每小题 5 分，共 80 分）

1. 欧欧喜欢吃鱿鱼。科学家表示，吃$ 10 $只虾和吃$ 3 $只鱿鱼的饱腹感相同。如果欧欧吃虾要吃$ 25 $只才能吃饱，那么他去海鲜餐厅吃鱿鱼，至少要点（ ）只鱿鱼才能吃饱。（只能点整数只鱿鱼）
   A. $7$
   B. $8$
   C. $9$
   D. $10$

2. 计算$ 314 \times 31.4 + 628 \times 68.6 + 68.6 \times 686 $的结果是（ ）。
   A. $6860$
   B. $100000$
   C. $31400$
   D. $62800$

3. 在乌龟毛毛失踪的这段时间，主人小朱好伤心，每天都为乌龟毛毛折纸鹤祈福，希望它早点找到回家的路。小朱第一天折了$ 30 $只，之后每天都比前一天多折$ 2 $只，当他折到第$ 210 $只纸鹤时，恰巧乌龟毛毛回来了。小朱一共折了（ ）天。
   A. $4$
   B. $5$
   C. $6$
   D. $7$

4. 万圣节晚上，为了烘托节日气氛，游乐场工作人员给整个场地安装了一种独特的南瓜灯，和一个会发出鬼怪叫声的喇叭。南瓜灯每$ 9 $分钟亮一次灯，而喇叭每到整点会发出叫声。晚上$ 18 $时整，喇叭发出声音且南瓜灯亮起，那么下一次既发声又亮灯的时间是（ ）。
   A. $19:00$
   B. $20:09$
   C. $21:00$
   D. $21:09$

5. 如图，一个正方体的六个面上分别写着六个连续的整数，且相对面上的两个整数的和都相等，将这个正方体放在桌面，将其按照如图所示的方式滚动，每滚动$ 90^\circ $算一次，那么滚动$ 2025 $次后，正方体贴在桌面一面的数字是（ ）。
   
   A. $7$
   B. $9$
   C. $10$
   D. $12$

6. 贝克是一名涂鸦艺术家，他使用喷漆、彩笔等工具，在公共空间（墙壁、隧道、桥梁等）进行创作，创作内容包括文字、图案、肖像等。如图所示，一块墙壁是由边长分别为$ 4 $分米和$ 6 $分米的两种正方形砖块拼接成，阴影部分为贝克涂鸦画的一部分图案，那么这个图案的面积为（ ）平方分米。
   
   A. $18$
   B. $20$
   C. $22$
   D. $24$

7. 古希腊著名的毕达哥拉斯学派把$ 1$，$ 4$，$ 9$，$ 16$……这样的数称为“正方形数”。正方形数都是一个自然数和自身相乘所得到的数。例如$ 64 $就是一个正方形数，因为$ 64=8 \times 8$。现在，有四个自然数，它们成等差数列。已知这四个数中有三个是正方形数，那么另外那个不是正方形数的最小是（ ）。
   
   A. $8$
   B. $5$
   C. $17$
   D. $24$

8. 小泉、小贝和小马缺席参加班上的数学测验，参加考试的同学的平均分是$ 56$。之后小泉补考了，平均分变成$ 60$；之后小贝补考了，平均分变成$ 59$；最后小马也补考了，平均分变成$ 62$。小泉、小贝和小马三人的平均分是$ 76$，小贝的得分是（ ）。
   A. $50$
   B. $51$
   C. $60$
   D. $68$

9. 某班在全校知识竞赛之前进行了三次模拟测验，每次测验全班$ 50 $位同学都参加。第一次测验不合格的有$ 8 $人，第二次测验合格的有$ 35 $人，第三次测验不合格的有$ 12 $人；已知全部三次皆合格的有$ 25 $人，只有两次合格的有$ 15 $人，三次都不合格的有（ ）人。
   A. $0$
   B. $1$
   C. $2$
   D. $3$

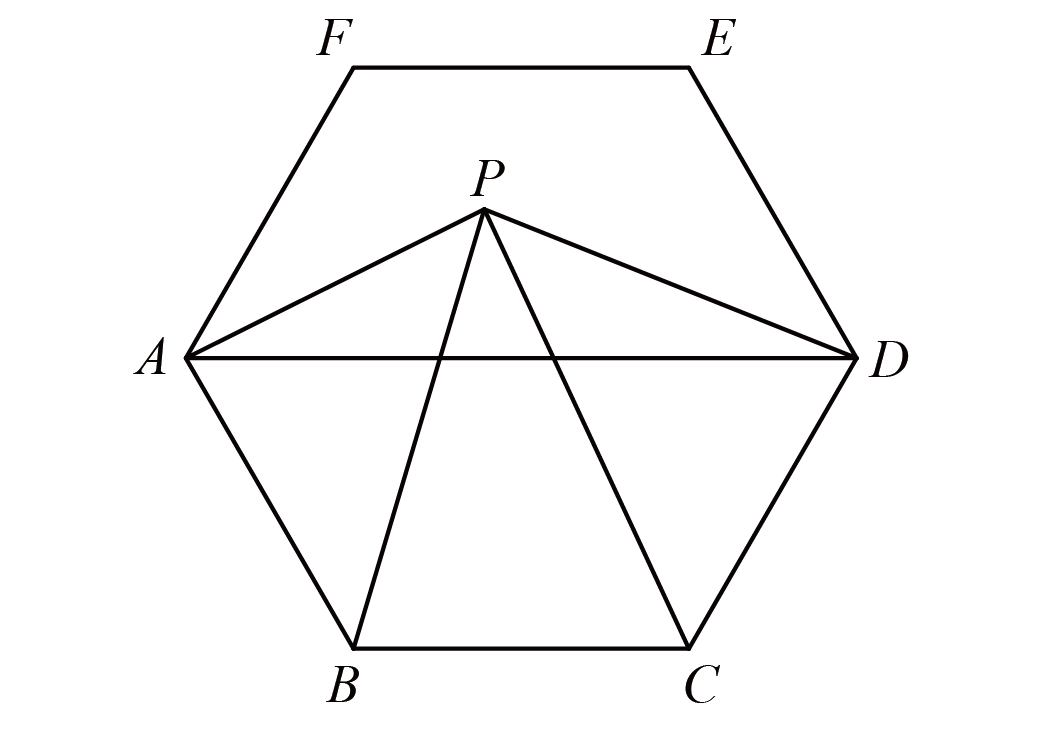
10. 夜幕降临一场激光表演开始，激光束在空中绘制出动态图案、文字甚至人物形象，不停地从一个图案巧妙地变换到另一个图案，吸引着一大群路人观看。如图所示，是激光束在空中变换时出现的图案，正方形$ ABCD $的边长是$ 8 $米，四边形$ EFGH $的面积是$ 5 $平方米，则图中阴影部分的面积是（ ）。
    
    A. $18$
    B. $22$
    C. $25$
    D. $32$

11. 五人参加象棋比赛，每两个人都要赛一局，规定：胜者得$ 2 $分，平局各得$ 1 $分，负者得$ 0 $分。比赛结果第一名两人并列，第四名两人并列，那么第三名得（ ）分。
    A. $1$
    B. $2$
    C. $3$
    D. $4$

12. 由于天气逐渐变冷，牧场上的牧草每天以均匀的速度在减少。牧场上的草可供$ 30 $头牛吃$ 8 $天；也可供$ 22 $头牛吃$ 10 $天。牧场上的草可供$ 10 $头牛吃（ ）天。
    A. $14$
    B. $16$
    C. $18$
    D. $20$

13. 五年级某班有$ 32 $位同学，从图书室共借取了$ 106 $本图书，每位同学借取图书的数量都不超过$ 6 $本。现在将同学按照借取图书的数量分组：没有借书的同学分为一组，借了$ 1 $本书的一组……依此类推。同学数量最多的一组最少有（ ）人。
    A. $4$
    B. $5$
    C. $6$
    D. $7$

14. 观察图中每一个大三角形中白色三角形的排列规律，则第$ 6 $个大三角形中白色三角形有（ ）个。
    
    A. $121$
    B. $243$
    C. $324$
    D. $364$

15. 甲、乙两人从$ A $地前往$ B $地，甲比乙早$ 40 $分钟出发，乙$ 1.5 $小时所到之处，甲$ 30 $分钟前刚好经过。此后乙速度增加$ 4 $千米$/$时，又经过$ 1.5 $小时追上甲。当乙到达$ B $地时，甲还距离$ B $地$ 6 $千米。那么$ A$、$B $两地相距（ ）千米。
    A. $66$
    B. $84$
    C. $90$
    D. $96$

16. 用$ 0 $和$ 1 $组成一个十位数（$0$，$1 $至少出现一次），没有孤立的$ 0$，且连续的$ 0 $都有偶数个，这样的十位数共有（ ）个。
    A. $34$
    B. $46$
    C. $49$
    D. $54$

二、解答题（每小题 10 分，共 40 分）

17. 小明家外墙墙面共计$ 300 $平方米，因整修需重刷防水漆。经过网搜寻价格后，发现两家评价不错、质量相当的品牌比较表如下：
    
    说明：
    i. 每升油漆大约可刷$ 10 $平方米的墙面。
    ii. 单人独立作业平均每小时可刷$ 25 $平方米的墙面。
    (1) 小明应该选择哪一品牌的防水漆比较便宜？（$3 $分）
    (2) 若选用较便宜的品牌，请问小明至少需购买几桶防水漆才会足够？（$3 $分）
    (3) 已知小明和爸爸、哥哥可合作刷墙面，若$ 3 $人速度相当且可以保持同样的速度进行，请问预估需要多少小时才能完工？（$4 $分）

18. 图中每个方格都代表一栋楼房，楼房有高有低，楼层数量在$ 1$~$4 $之间。箭头中的数字表示从箭头方看时，能看到的楼房数量。同一方向上楼层低的楼房会被前面楼层高的楼房完全遮挡。请将每栋楼房的楼层数（$1$~$4 $填入方格里，所填数字在每行和每列中不能重复出现。
    
    (1) 第四行第一列方格里的数是$\underline{\quad \quad} $。（$3 $分）
    (2) 第三行第二列方格里的数是$\underline{\quad \quad} $。（$3 $分）
    (3) 第一行四个方格里的数从左到右分别是$\underline{\quad \quad} $、$\underline{\quad \quad} $、$\underline{\quad \quad} $、$\underline{\quad \quad} $。（$4 $分）

19. 甲、乙、丙三人同时从$ A $地出发前往$ B $地，$AB $两地相距$ 36 $千米。现有一辆自行车，他们三人决定：甲先骑自行车乘载乙，丙步行。当甲、乙到达$ C $地时，乙下车步行前往$ B $地，此时甲立即沿原路返回去接丙。甲在$ D $地与丙相遇，然后甲、丙两人同乘自行车前往$ B $地。结果三人同时到达$ B $地。已知乙、丙两人的步行速度相同，并且自行车的速度比步行速度快两倍。
    (1) $D $地距$ A $地多少千米？（$5 $分）
    (2) $C $地距$ A $地多少千米？（$5 $分）

20. 码头上有一些不同规格的货物集装箱，它们是由若干个大小相同的正方形小集装箱组成。仓库每行左面的数表示该行小集装箱的数量，仓库下面的数字表示该列小集装箱的数量。
    集装箱摆放规则：
    ① 集装箱不能重叠摆放，也不能拆分开摆放；
    ② 每个集装箱相邻的方格中不能再摆放集装箱（如图$ 1$）。
    图$ 2 $中有$ 4 $种规格的集装箱共$ 10 $个，请根据以上规则在图$ 2 $的仓库中画出集装箱的位置。（$10 $分）