2025.12.21华杯赛小高组-邱福星的教学页面

2025.12.21华杯赛小高组

1月7日 10:44更新

01458

如果$a \oplus b = 3a + 5b$，$a \otimes b = 3ab$，那么在$(3 \oplus x) \otimes 3 = 81$中，$x = \underline{\quad \quad} $．

$0$
令$y=3\oplus x$，原式为$y \otimes 3 = 81$，即$3 \times y \times 3 = 81$，$y = 9$；
$3 \oplus x = 9$，即$3 \times 3 + 5x = 9$，$x = 0$．

在一个水池中有两根直立的木棍，每根木棍的一端都紧贴着池底，另一端都露在水面上．两个木棍露出水面部分的长度之比是$10:7$．如果现在水池中的水面向下降$35$厘米，则两根木棍露出水面的部分的长度之比是$9:7$．那么原来这两根木棍露出水面部分的长度和是$ \underline{\quad \quad} $厘米．

$170$
水面下降，两根木棍露出水面部分的差不变，令两根木棍分别为$A$和$B$
原$A:B:$差 $= 10:7:3=20:14:6$
现$A:B:$差 $= 9:7:2=27:21:6$
$1$份：$35 \div (27 – 20) = 5\rm \text{cm}$，原长度和：$(20 + 14) \times 5 = 170\rm \text{cm}$．

在一个不透明的口袋中，装有$6$个红球，$3$个白球和$7$个黑球．这些球除了颜色不同外，其他都相同．现从中任意摸出一个小球，要使摸到红球的可能性为$60\%$，则需要往这个口袋再放入同样的红球$ \underline{\quad \quad} $个．

$9$
可能性为$60\%$，指最终袋子中红球占$60\%$
法$1$，白黑不变，最终占$1-60\%=40\%$，最终袋子中有$(3+7)\div 40\%=25$个，红球再放$25-6-3-7=9$个．
法$2$，设再放$x$个红球，$(6+x)=(6+3+7+x)\times 60\%$，$x=9$．

一个由不同数字组成的四位数$\overline{2\square3\square}$能同时被$8$、$9$整除，那么这个四位数是$ \underline{\quad \quad} $．

$2736$
$8$的倍数特征为末三位，但末三位均未知．考虑到$8$的倍数必为$4$的倍数，先观察末两位，$\overline{3\square}$为$4$的倍数，$\square$只能为$2$或$6$，其中$2$与原数千位“$2$”重复，只能为$6$．
题目变为：$\overline{2\square36}$为$9$的倍数，通过数字和可得百位$\square$为$7$．
再次验证$736$为$8$的倍数，答案为$2736$．

计算：$1+(1+3)+(1+3+5)+(1+3+5+7)+\cdots+(1+3+5+\cdots+99)= \underline{\quad \quad} $．

$42925$
每个括号内为从$1$开始的连续奇数求和，即项数的平方
原式$=1^2+2^2+3^2+4^2+\cdots+50^2=\dfrac{1}{6}\times 50\times 51\times 101=42925.$
（注：从$1$开始连续自然数平方和$1^2+2^2+3^2+\cdots+n^2=\dfrac{1}{6}\times n\times (n+1)\times (2n+1)$）

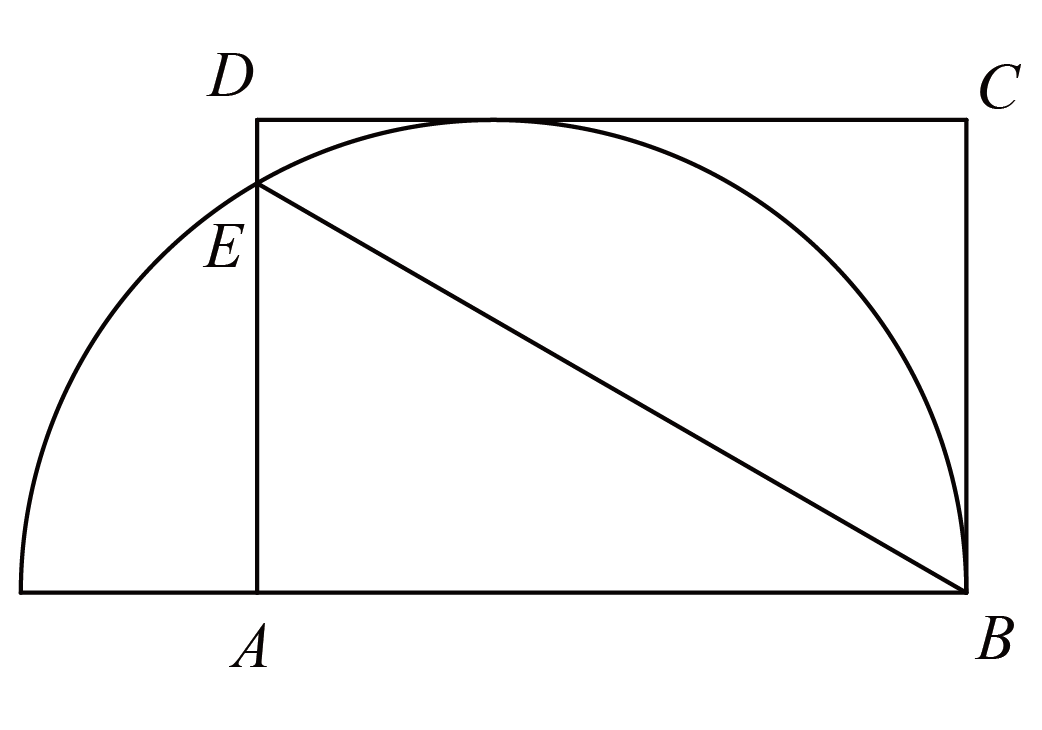
小红从$A$点出发，按“$A-D-E-F-B-A\cdots$”的顺序在五边形跑道上练习跑步，与此同时，小雨从点$B$出发，按“$B-C-D-A-B\cdots$”的顺序在正方形跑道上练习跑步，已知$AB$为$54$米，$F$为$BC$中点．又知小红与小雨的速度比为$4:5$，且两人第一次相遇时恰好在$E$点．那么$DE$的长为$ \underline{\quad \quad} $米．

$18$
本题难点在于判断是否小红第一次到$E$时恰好为两人第一次相遇
①假设小红第一次到$E$时，两人第一次相遇．

路程和为$54 \times 3 = 162\rm m$，速度比为$4:5$，则路程比为$4:5$，$AD + DE = 162 \div (5 + 4) \times 4 = 72\rm m$，$DE = 72 – 54 = 18\rm m$．
②若$DE>18$，小雨到达$E$时，小红还未到达$E$，必在$DE$之间相遇，与题意矛盾．

③若$DE<18$，小红到达$E$时，小雨还未到达$E$（如图$1$），继续前行，必在$E-D-A-B-F$之间相遇（如图$2$），与题意矛盾．

自然数$n$共有$1001$个因数，则$n$的最小值为$ \underline{\quad \quad} $．（可以用指数乘积的形式表示）

$2^{12}\times3^{10}\times5^6$
因数个数为（指数$+1$）再连乘，考虑$n$的质因数种类
一种质因数：$1001=1001$，$n=\Box^{1000}$，最小为$2^{1000}$；
两种质因数：$1001=7\times143$，$n=\Box^6\times\Box^{142}$，最小为$3^6\times2^{142}$；
$1001=11\times91$，$n=\Box^{10}\times\Box^{90}$，最小为$3^{10}\times2^{90}$；
$1001=13\times77$，$n=\Box^{12}\times\Box^{76}$，最小为$3^{12}\times2^{76}$；
三种质因数：$1001=7\times11\times13$，$n=\Box^6\times\Box^{10}\times\Box^{12}$，最小为$5^6\times3^{10}\times2^{12}$；
显然，$2^{12}\times3^{10}\times5^6$最小．

把$7$个人分成$4$组，每组至少一人，不区分组序，共有$ \underline{\quad \quad} $种分法．

$350$
把不同元素分组，可以使用乘法原理分步选择，不考虑组序，则相同数量的组需要除序．
首先分配数量，$7$人分$4$组，每组至少$1$人，数量可能为：$4111$、$3211$、$2221$．
①$4111$，先选$4$人，后续$3$人自动分组，有$\text{C}_7^4=35$种；
②$3211$，先选$3$人，再选$2$人，后续$2$人自动分组，$3$、$2$数量不同无需除序，有$\text{C}_7^3\times \text{C}_4^2=35\times 6=210$种；
③$2221$，先选$2$人，再选$2$人，再选$2$人，后续$1$人自动分组，$2$、$2$、$2$数量相同需要除序，有$\dfrac{\text{C}_7^2\times \text{C}_5^2\times \text{C}_3^2}{\text{A}_3^3}=\dfrac{21\times 10\times 3}{6}=105$种；
共$35+210+105=350$种．

把一个大长方体木块表面上涂满红色后，分割成若干个棱长为$1$的小正方体，若其中恰有两个面涂上红色的小正方体恰好是$2025$块，则大长方体体积取值最小时，大长方体的表面积是$ \underline{\quad \quad} $．

$4606$
染色问题有以下规律：
若为$1 \times 1 \times a (a > 2)$型，则两端染$5$面，中间染$4$面；
若为$1 \times a \times b (a > 2$、$b$ $> 2)$型，则顶点染$4$面，棱中染$3$面，面中染$2$面；
若为$a \times b \times c (a > 2$、$b> 2$、$c> 2)$型，则顶点染$3$面，棱中染$2$面，面中染$1$面，体中染$0$面；
此题染$2$面，只能为后$2$种情况，且第$3$种情况染$2$面的个数为$4(a – 2 + b – 2 + c – 2)$为$4$的倍数，不为$2025$，排除．
故只能为$1 \times a \times b (a > 2$、$b$ $> 2)$形，两面个数为$(a – 2)(b – 2) = 2025$，易得：
$\begin{cases}a – 2 = 1 \\b – 2 = 2025\end{cases}$，$\begin{cases}a – 2 = 3 \\b – 2 = 675\end{cases}\cdots \cdots \begin{cases}a – 2 = 45 \\b – 2 = 45\end{cases}$，即
$\begin{cases}a = 3 \\b = 2027\end{cases}$，$\begin{cases}a = 5 \\b = 677\end{cases}\cdots \cdots \begin{cases}a = 47 \\b = 47\end{cases}$，验证可得$\begin{cases}a = 47 \\b = 47\end{cases}$时体积最小，
此时表面积为$(1 \times 47 + 1 \times 47 + 47 \times 47) \times 2 = 4606$．

某校六年级数学、编程两个兴趣小组共$48$人去图书馆借阅图书．其中，数学兴趣小组的同学平均每人借了$4$本书，编程兴趣小组的同学平均每人借了$3.5$本书，既参加了数学兴趣小组又参加了编程兴趣小组的同学平均每人借了$6.2$本书，且两个兴趣小组总共向图书馆借了$168$本书．那么既参加了数学兴趣小组又参加了编程兴趣小组的同学有$ \underline{\quad \quad} $人．

$5$
此题有容斥背景，画图如下（设只参加数学$a$人，均参加$b$人，只参加编程$c$人）

有$\begin{cases}a+b+c=48 ① \\4(a+b)+3.5(b+c)-6.2b=168 ②\end{cases}$
②化简得$4a+3.5c+1.3b=168$，系数整数化$40a+35c+13b=1680 $③
①$\times40-$③得：$5c+27b=240$，
$5c$、$240$均为$5$的倍数，故$27b$也为$5$的倍数，$b$为$5$，
解不定方程得：$\begin{cases}b=5 \\c=21\end{cases}$，且无其他解，故均参加的有$5$人．

对任意正整数$m$，$n$，定义：$r(m$，$n)$为$m\div n$的余数（比如$r(8$，$3)=2$），那么满足方程：$r(m$，$1)+r(m$，$2)+r(m$，$3)+\cdots +r(m$，$10)=4$的最小正整数解是$ \underline{\quad \quad} $．

$120$
题意为除以$1\sim10$后余数总和为$4$的最小自然数，需分配余数．且大合数的余数与其因数的余数等价，如$8$、$4$、$2$相互关联，$9$、$3$相互关联，$10$、$5$、$2$相互关联，$6$、$3$、$2$相互关联，分步讨论如下：
①此数若为奇数，则除以$2$、$4$、$6$、$8$、$10$均至少余$1$，不符，故此数必为偶数．考虑$8$的余数，只能为$4$、$2$、$0$（$6>4$，排除）；
若余$4$，则其他均余$0$，至少为$[1$，$2$，$3$，$4$，$5$，$6$，$7$，$9$，$10]=1260$，此时恰除以$8$余$4$；
若余$2$，则除以$4$也余$2$，其他均余$0$，至少为$[1$，$2$，$3$，$5$，$6$，$7$，$9$，$10]=630$，
此时除以$8$余$6$，再向后枚举为$630\times2=1260$同上，再后$630\times3>1260$，排除；
若余$0$，则除以$4$、$2$均余$0$，再考虑其他．
②考虑$9$的余数，只能为$4$、$3$、$2$、$1$、$0$
若余$4$，则除以$3$余$1$，排除；
若余$3$，则除以$3$余$0$，且除以$6$余$0$（$m$为偶数），剩余$1$考虑$5$或$7$的余数，
若除以$5$余$1$，则除以$10$也余$1$，排除，只能除以$7$余$1$，
至少为$[1$，$2$，$3$，$4$，$5$，$6$，$8$，$10]=120$，此时恰除以$9$余$3$、除以$7$余$1$；
若余$2$，则除以$3$余$2$，除以$6$余$2$（除以$3$余$2$，除以$2$余$0$），排除；
若余$1$，则除以$3$余$1$，除以$6$余$4$（除以$3$余$1$，除以$2$余$0$），排除；
若余$0$，则除以$3$余$0$，除以$6$余$0$，则此数必为$[1$，$2$，$3$，$4$，$6$，$8$，$9]=72$的倍数；
$72$除以$5$、$7$、$10$均余$2$排除，$72$的$2$倍$=144>120$，故后续不用讨论．
综上：$m$最小为$120$．

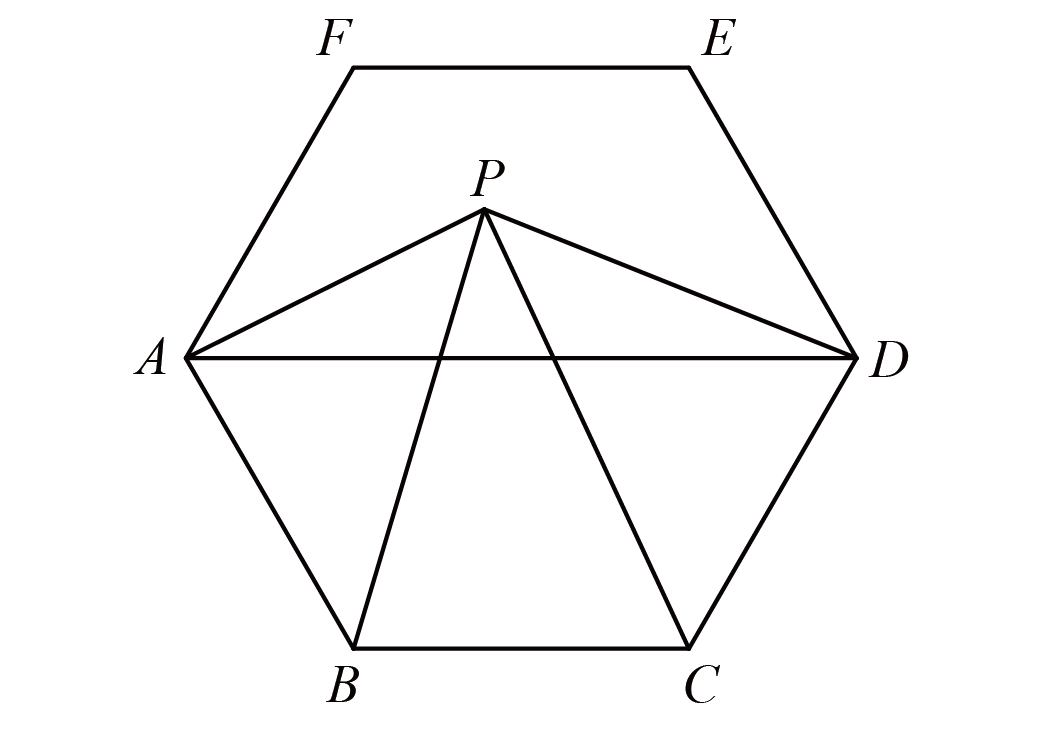
如图，正六边形$ABCDEF$的面积是$45$平方厘米，$G$点是边$AF$的中点，$GD$与$FC$相交于$O$点，连接$AO$并延长与边$DE$相交于$H$点．

$(1)\triangle GCD$的面积是$ \underline{\quad \quad} $平方厘米．
$(2)\triangle GCO$的面积是$ \underline{\quad \quad} $平方厘米．
$(3)\triangle ODH$的面积是$ \underline{\quad \quad} $平方厘米．

$15$、$ 5$、$5$
$(1)$阴影长方形占正六边形的$\dfrac{2}{3}$，故$\triangle GCD$占长方形的$\dfrac{1}{2}$，$S_{\triangle GCD}=45\times\dfrac{2}{3}\times\dfrac{1}{2}=15$．

(2)在沙漏$GFOCD$中$\dfrac{GO}{OD}=\dfrac{FO}{OC}=\dfrac{GF}{CD}=\dfrac{1}{2}$，由等高模型$S_{\triangle GCO}=S_{\triangle GCD}\times \dfrac{1}{3}=15\times \dfrac{1}{3}=5$．

(3)③此问方法较多，提供一种辅助线较少的方法：
$\triangle ODH$与$\triangle AOG$成共角模型，且$GO:OD=2:1$，$AO:OH=1:1$，故先求$\triangle AOG$
$S_{\triangle GFO}=S_{\triangle GCO}\times\dfrac{1}{2}=2.5$，$S_{\triangle AGO}=S_{\triangle GFO}=2.5$；

$\dfrac{S_{\triangle AGO}}{S_{\triangle ODH}}=\dfrac{1\times 1}{1\times 2}=\dfrac{1}{2}$，$S_{\triangle ODH}=2S_{\triangle AGO}=2.5\times 2=5.$
说明：$AB // FC // DE$，
$\triangle AO^{\prime}O$与$\triangle ADH$成金字塔模型
$\dfrac{AO}{OH}=\dfrac{AO^{\prime}}{O^{\prime}D}=\dfrac{1}{1}$．

© 版权声明

部分题目来自网络，如有侵权，请联系删除

THE END

未分类
# 华杯赛

喜欢就支持一下吧

相关推荐

评论抢沙发

欢迎做题

提交

暂无评论内容