- 杭州某服装厂计划做$ 300 $套$ G20 $峰会上使用的舞蹈服装,在完成计划的$ 20\%$之后,改进了裁剪方法,每套节约用 十三分之一 ,把节约下来的布用新的裁剪方法做,可以多做多少套?
- $20$
- 剩:$ 300 \times (1-20\%) = 240 $(套)
$240 \div (1 – \dfrac{1}{13}) = 260 $(套)
多$ 260 – 240 = 20 $(套)
- 一项工程,甲单独干$ 12 $天可以完成,乙单独干$ 15 $天可以完成,两人合作若干天后,甲被调走,剩下的工程由乙独自完成,乙干了$ 3 $天后,为了早点完工,将自己的工作效率提高了$ 2\%$,又用了$ 6 $天时间完成剩下的工程,则甲干了多少天?
- $2$
- $V_{\text{$甲$}} = \dfrac{1}{12} \quad V_{\text{$乙$}} = \dfrac{1}{15} \quad V$’$_{\text{$乙$}} = \dfrac{1}{15} \times (1+25\%) = \dfrac{1}{12}$
乙干了$ \dfrac{1}{15} \times 3 + \dfrac{1}{12} \times 6 = \dfrac{1}{5} + \dfrac{1}{2} = \dfrac{7}{10}$
甲干了$ (1 – \dfrac{7}{10}) \div (\dfrac{1}{12} + \dfrac{1}{15}) = \dfrac{3}{10} \div \dfrac{9}{60} = \dfrac{3}{10} \times \dfrac{60}{9} = 2 $(天)
- 在一个$ 800m $的环形跑道上,兄弟两人同时从同一起点按顺时针方向跑步,两人每隔$ 20 $分钟相遇一次,若两人的速度不变还是在原来的出发点同时出发,哥哥改为按逆时针方向跑,则两人每隔$ 5 $分钟相遇一次,两人跑一圈各要多少分钟?
- $8$、$\dfrac{40}{3} $
- $\begin{cases} V_{\text{$甲$}} – V_{\text{$乙$}} = 800 \div 20 = 40 \ V_{\text{$甲$}} + V_{\text{$乙$}} = 800 \div 5 = 160 \end{cases}$
$\begin{cases} V_{\text{$甲$}} = 100 \ V_{\text{$乙$}} = 60 \end{cases}$
$t_{\text{$甲$}} = 800 \div 100 = 8 $(分)
$t_{\text{$乙$}} = 800 \div 60 = \dfrac{40}{3} $(分)
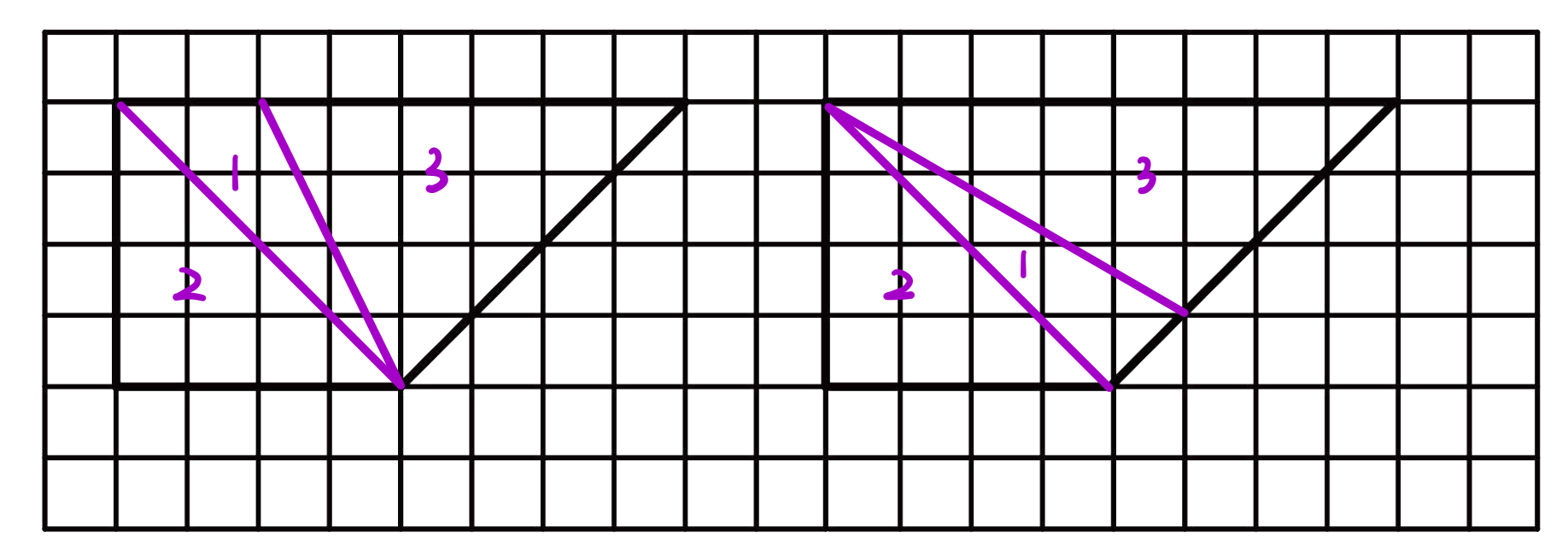
- 由边长相等的小正方形组成的网格中有一个梯形,请你用两种不同的方法把这个梯形分为$ 3 $个三角形,使$ 3 $个三角形的面积比是$ 1:2:3$。
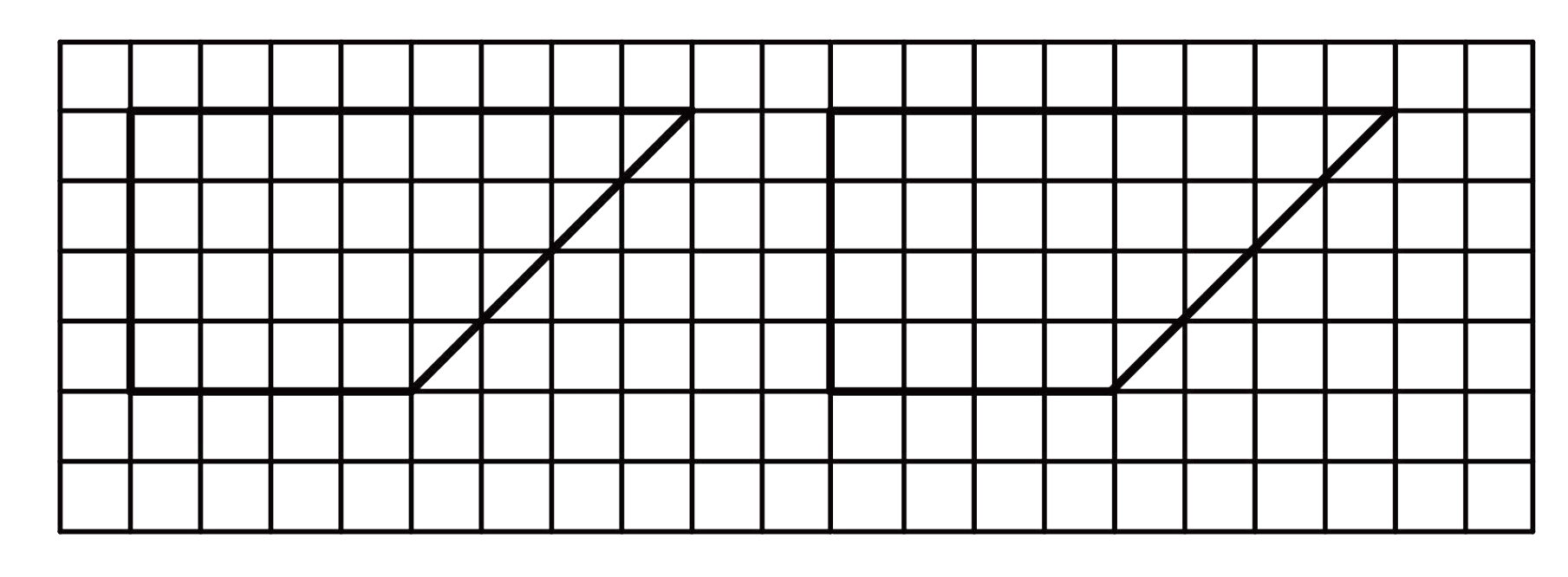
- 如图
- $4:8 = 1:2 = 2:(1+3)$
方法不唯一
先分成$ 1:2 $两个部分
再将较大的分成$ 1:3 $即可
- 观察下面的规律并回答问题:
我们发现这组数$ 4$,$ 7$,$ 31$,$ 49$,$ 103$, 其中任意三个数之和都是$ 3 $的倍数。而$ 6$,$ 10$,$ 22$,$ 42$,$ 54$, 这组数中任意$ 4 $个数之和都是$ 4 $的倍数。
问题一、请你自己再写出$ 5 $个正整数,它们都不是$ 3 $的倍数,但是任意$ 3 $数之和是$ 3 $的倍数。(不能与题干的示例相同)
问题二、有$ 10 $个不相等的正整数,其中任意$ 4 $个数之和都是$ 4 $的倍数,若其中有一个数是$ 14$,则这$ 10 $个数的和最小值是多少。
问题三、对于一列整数$ a_1$,$ a_2$,$ \dots$,$ a_n$,若 $1=a_1 < a_2 < \dots < a_n = 2026$,这$ n $个整数中任意$ (n-1) $个数的和都是$ (n-1) $的倍数,则$ n $的最大值为多少。
- 见解析
- $(1)\div 3 \cdots 2 $即可
$2$,$ 5$,$ 8$,$ 11$,$ 14$
$(2)14 \div 4 \cdots 2$
$2 + 6 + 10 + 14 + \cdots + 38 = (2+38) \times 10 \div 2 = 200$
(3)$a_1 < a_2 < \dots < a_n$
记$ S_n = a_1 + a_2 + \dots + a_n$
则$ n-1 \mid S_n – a_i$
则$ S_n \equiv a_i \pmod{n-1}$
则每个数除以$ n-1 $余数相同
$a_1 \div (n-1) \dots 1 $余数都为$ 1$
要想$ n $最大,相邻两数最少差$ n-1$
$a_1 \quad a_2 \quad a_3 \quad \dots \quad a_n$
$1 \quad n \quad 2n-1 \quad \dots \quad 2026$
$1 + (n-1)^2 = 2026$
$(n-1) = 45$
$n = 46$
- 定义:对于一组互不相等的数,若对于其中任意两个数$ a$,$ b$,$a+b $与$ a-b(a>b) $两数中至少有一个在这组数中,则称这组数是“好数组”。
(1) 判断:$2$,$ 3$, $5\underline{\quad \quad}$“好数组”,$1$,$ 2$,$ 3$, $5\underline{\quad \quad}$“好数组”;(填“是”或“不是”)
(2) 若$ 2$,$ 4$,$ 8$,$ x $是“好数组”,求出$ x $的所有可能值;
(3) 若含$ 2025 $的$ 5 $个正数是“好数组”,求出所有符合条件的“好数组”。
- 见解析
- (1)是、$1+5=6 \quad 5-1=4 $都不在,所以不是
(2)极端分析
$2+8=10 \quad 8-2=6 \quad $故$ x=6 $或$ 10$
$2$,$ 4$,$ 8$,$ 10 \quad 4+10=14 \quad 10-4=6 $都不在
$\therefore x=6 $验证成立
(3)设 $a < b < c < d < e$
$a+e$,$ \ b+e$,$ \ c+e$,$ \ d+e $肯定不在这组数中
则 $e-d < e-c < e-b < e-a$ 在这组数中
$\begin{cases} e-d=a \\ e-c=b \\ e-b=c \\ e-a=d \end{cases} \Rightarrow \begin{cases} a+d=e \\ b+c=e \end{cases}$
$b+d a+d=e $则$ d-b $在其中
$c+d a+d=e $则$ d-c $在其中
$e-b>d-b>d-c$,这三个数就分别是$c$、$b$、$a$
$\therefore \begin{cases} d-b=b \\ d-c=a \end{cases} \Rightarrow \begin{cases} d=2b \\ a+c=d \end{cases} \Rightarrow a+c=2b \quad $则$a$,$ b$,$ c $等差
$a+d=b+c \Rightarrow d-c = b-a = a \quad e-d=a$
$\therefore a$,$ b$,$ c$,$ d$,$ e $等差且公差为$ a$
$\therefore $这$ 5 $个数是$ a$,$ 2a$,$ 3a$,$ 4a$,$ 5a $其中一个为$ 2025$
(1) $a = 2025: 2025$,$ 4050$,$ 6075$,$ 8100$,$ 10125$
(2) $2a = 2025: \dfrac{2025}{2}$,$ 2025$,$ \dfrac{6075}{2}$,$ 4050$,$ \dfrac{10125}{2}$
(3) $3a = 2025: 675$,$ 1350$,$ 2025$,$ 2700$,$ 3375$
(4) $4a = 2025: \dfrac{2025}{4}$,$ \dfrac{2025}{2}$,$ \dfrac{6075}{4}$,$ 2025$,$ \dfrac{10125}{4}$
(5) $5a = 2025: 405$,$ 810$,$ 1215$,$ 1620$,$ 2025$
© 版权声明
部分题目来自网络,如有侵权,请联系删除
THE END













暂无评论内容