2026经开外校选拔考试

数学试卷（一试）

时间：2 小时 试卷满分：一试 80 分 + 加试 100 分

填空题，只得出最后结果（每小题 5 分，共 80 分）

1. 计算：$0.125 \times 3\dfrac{1}{7} \times 12.5\% \div \dfrac{4}{15} + 8 = \underline{\quad \quad} $。

2. 计算：$\dfrac{20252026^2}{20252025^2 + 20252027^2 – 2} = \underline{\quad \quad} $。

3. 一次测试一共有$ 24 $道题，其中$ 10 $道选择，$8 $道填空，$6 $道解答。已知选择、空每小题分值相同，测试满分是$ 120 $分，小明选择题的得分占选择题总分的$ 90\%$，填空题的得分占填空题总分的$ \dfrac{8}{11}$，解答题的得分占解答题总分的$ \dfrac{7}{12}$，小明总分为$ 109 $分，那么解答题的总分是$ \underline{\quad \quad} $分。

4. 某工厂甲、乙两车间的人数比是$ 2:3$，因工作需要，甲车间新调入$ 36 $人，现在两车间的人数比是$ 4:5$，现在甲车间人数比乙车间少$ \underline{\quad \quad} $人。

5. 一批衣服打算以$ 30\% $的利润卖出，卖了$ 70\% $后打折，全部衣服卖完后的总利润只有不打折售卖利润的$ 74\%$，则打了$ \underline{\quad \quad} $折。

6. 如图，直径为$ 6 $厘米的半圆绕点$ A $逆时针旋转$ 60^\circ $使$ AB $到达$ AC $的位置，求图中阴影部分的周长是$ \underline{\quad \quad} \text{cm}$，面积是$ \underline{\quad \quad} \text{cm}^2$。
   

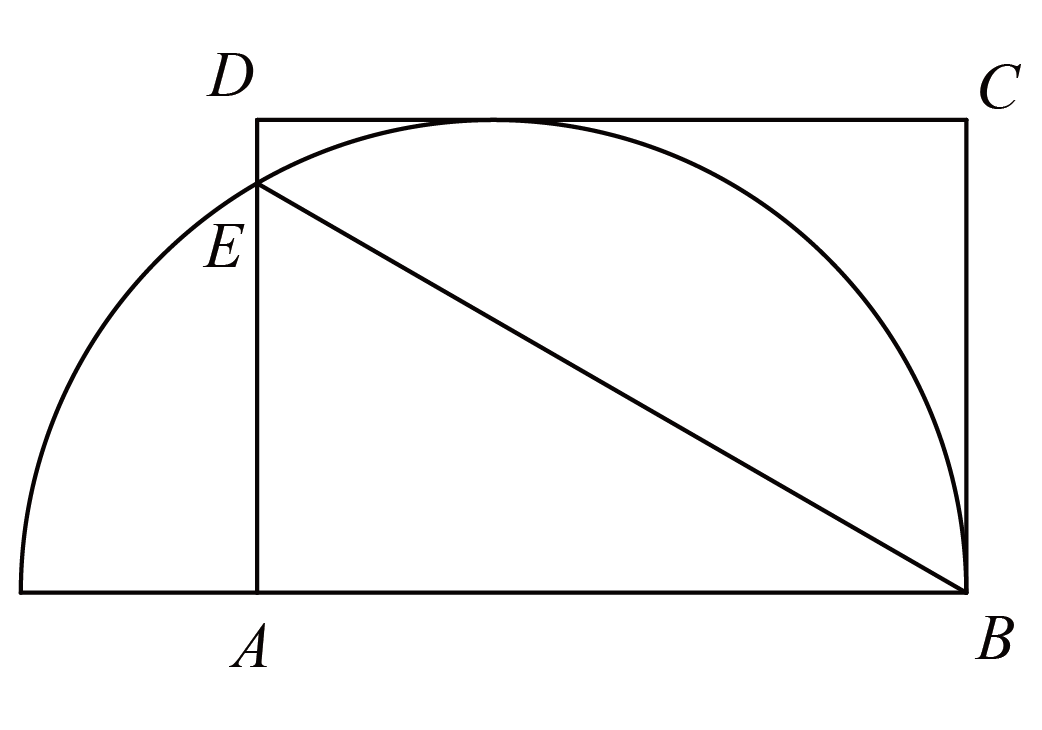
7. 先把一张正方形纸片对折，再沿着下图中的虚线进行折叠，使$ A $点恰好落在中线上，那么$ \angle ABE = \underline{\quad \quad} $度。
   

8. 大于$ 1 $的正整数$ m $的三次幂可“分裂”成$ m $个连续奇数的和，如：$2^3=3+5$，$ 3^3=7+9+11$，$ 4^3=13+15+17+19$，$… $若$ m^3 $“分裂”后，其中有一个奇数是$ 2031$，则$ m $的值是$ \underline{\quad \quad} $。

9. 将$ 1 $个$ 1$，$2 $个$ 2$，$3 $个$ 3$，$…$，$2026 $个$ 2026 $排成一列，那么这列数的第$ 2026 $个数是$ \underline{\quad \quad} $。

10. 甲、乙两人分别从$ A$、$B $两地同时出发，相向而行，出发时他们的速度比是$ 3:2$，第一次相遇后，甲提速$ 20\%$，乙提速$ 30\%$，这样当甲到达$ B $地时，乙离$ A $地还有$ 14 $千米，$A$、$B $相距$ \underline{\quad \quad} $千米。

11. 如图，三角形$ ABC $中，$ AF:FD=2:1$，$ BF:FE=3:1$，那么$ S_{\triangle ABC} = \underline{\quad \quad} S_{\triangle FDC}$。
    

12. 甲、乙、丙、丁、戊五位同学各写了一张贺卡，打乱顺序后，每人拿一张，则恰好只有一个人拿到自己写的贺卡的情形有$ \underline{\quad \quad} $种。

13. 已知$ 1^2+2^2+3^2+\dots+n^2 = \dfrac{1}{6}n(n+1)(2n+1)$，$1^3+2^3+3^3+\dots+n^3 = \dfrac{n^2(n+1)^2}{4}$，试计算：
    $ \dfrac{1^2+2^2+3^2}{1^3+2^3+3^3} + \dfrac{1^2+2^2+3^2+4^2}{1^3+2^3+3^3+4^3} + \dots + \dfrac{1^2+2^2+3^2+\dots+2026^2}{1^3+2^3+3^3+\dots+2026^3} $的值是$ \underline{\quad \quad} $。

14. 对于一些数$ a_1$，$ a_2$，$ \dots$，$ a_n$，若$ a_i > a_j$，且 $i < j$，则称 $a_i$ 和 $a_j$ 逆序，$(a_i， a_j)$ 是一组逆序数对， $a_{1}$到 $a_{n}$ 中逆序数对的数量叫逆序数。已知 $101$ 个互不相同的整数分别为 $a_1 \sim a_{101}$，若排列$ a_1$，$ a_2$， $\dots$， $a_{101}$ 的逆序数为 $2026$，那么按照 $a_{101}$， $a_{100}$， $\dots$， $a_1$ 的排序，逆序数是 $\underline{\quad \quad}$ 。

15. 从三位数$ 100$~$999 $中任取出$ n $个不同的数，使得总能找到其中的$ 3 $个数，它们的数字和相同，那么$ n $的最小值为$ \underline{\quad \quad} $。

16. 将$ 1-2049 $这$ 2049 $个数从左到右写成一行，之后每次都将最左边的两个数擦掉，并将这两个数的差写在这列数的最后右边，就这样一擦一写，写数，那么当只剩下$ 2 $个数时，这两个数的差是$ \underline{\quad \quad} $。

数学试卷（二试）

1. （本题满分$ 20 $分）进制转换（解答题，需写出必要过程）
   （此处为关于进制的介绍文本，大意如下：）
   我们日常用的数是十进制，即逢十进一。十进制表示某一位置上的数运算时是$ 10 $的$ n $次方。
   十进制如：十进制是逢十进一，十六进制是逢十六进一，二进制是逢二进一，以此类推。
   常见的制有：十进制，二进制，十六进制，十二进制，二十进制等。
   我们在日常常用的进制为十进制，为了区别其他进制，进制书写过程中通常在数的右下角标上基数，比如：二进制数$ (1110)_2$，$(2310)_7 $等。
   计算机利用的是二进制数，它共有两个数码$ 0$，$1$。将一个十进制数转化为二进制，只需把该数写成若干个$ 2^n $数的和，依次写出$ 1 $或$ 0 $即可。如$ 19$
   $ 19 = 1 \times 2^4 + 0 \times 2^3 + 0 \times 2^2 + 1 \times 2^1 + 1 = (10011)_2 $为二进制下的五位数。
   (1) 十进制$ 1025 $是二进制下的$ \underline{\quad \quad} $位数；
   (2) 一个四位数四个数位的取值只有$ 0-6$，将这些四位数从小到大排列，求$ 2026 $是第几个？
   (3) 现有六个筹码，上面分别写有数值：$1$，$ 3$，$ 9$，$ 27$，$ 81$，$ 243$，任意搭配这些筹码（也可以只选择$ 1 $个筹码）可以得到多少个不同的和？将这些和加起来，总和为多少？将这些和从小到大排列起来，第$ 40 $个是多少？

2. （本题满分$ 20 $分）用$ [x] $表示不大于$ x $的最大整数，$ {x} = x – [x]$，比如$ [3.7]=3$，$ {3.7}=0.7$
   $ (1) \left[ \dfrac{200 \times 1}{2027} \right]$，$ \left[ \dfrac{200 \times 2}{2027} \right]$，$ \dots$，$ \left[ \dfrac{200 \times 2026}{2027} \right] $的值等于$ \underline{\quad \quad} $。
   (2) 求$\left[ \dfrac{10^{20000} }{10^{100} +3} \right] $的个位；
   (3) 在$ \left[ \dfrac{2025}{1} \right]$，$ \left[ \dfrac{2024}{2} \right]$，$ \left[ \dfrac{2023}{3} \right]$，$ \dots$，$ \left[ \dfrac{1}{2025} \right] $中，有多少个不同的整数？

3. （本题满分$ 20 $分）如图是一个$ 4 \times 5 $的方格盘，先将其中的$ 4 $个方格染黑，然后按以下规则继续染色：如果某个未染色的方格有两个黑色的公共边，就将这个方格染黑。这样操作下去，能否将整个方格盘都染成黑色？
   

4. （本题满分$ 20 $分）$10 $名乒乓球选手进行单循环比赛（每两个人之间均赛一场），用$ x_i$，$ y_i $顺次表示第一号选手胜与负的场数，用$ x_2$，$ y_2 $表示第二位选手胜与负的场数，$……$，用$ x_{10}$，$ y_{10} $表示第十位选手胜与负的场数。求证：
   $ x_1^2 + x_2^2 + \dots + x_{10}^2 = y_1^2 + y_2^2 + \dots + y_{10}^2$。

5. （本题满分$ 20 $分）某俱乐部的共有$ 100 $名成员，每一名成员都声称你愿意和自己认识的人一起打篮球，已知每名成员都至少认识$ 67 $名成员。证明：一定有$ 4 $名成员，他们可以可以在一起打篮球。