2026年华数冬令营（香港营）小高年级组

注意事项： 1、试卷共$18$道题，考试时间$120$分钟；$ 2$、请把答案写到相应答题区域。

一、填空题（共12题，每题10分，共120分）

1. 算式$ \dfrac{202626^2}{2} \times \left( \dfrac{405249^2}{202624 \times 202625 \times 202626} – \dfrac{202625}{202624 \times 202626} – \dfrac{202624}{202625 \times 202626} \right) $的计算结果是$\underline{\quad \quad} $。

• $202626$
• 原式$= \dfrac{202626^2}{2} \times \dfrac{405249^2 – 202625^2 – 202624^2}{202624 \times 202625 \times 202626}$
  $= \dfrac{202626^2}{2} \times \dfrac{(202624+202625)^2 – 202625^2 – 202624^2}{202624 \times 202625 \times 202626}$
  $= \dfrac{202626}{2} \times \dfrac{2 \times 202624 \times 202625}{202624 \times 202625}$
  $= 202626$

2. 甲、乙、丙、丁参加四项体育项目，每一项的第一名加$5$分，第二名加$3$分，第三名加$2$分，第四名加$1$分，没有并列的。甲是第一名，总共$18$分，乙是第二名，总共$12$分，那么丙最多能得到$\underline{\quad \quad} $分。

• $10$
• $18 = 5+5+5+3$；$12 = 5+3+3+1=5+3+2+2$
  甲：$5$，$ 5$，$ 5$，$ 3 (18$分$)$
  乙：$3$，$ 2$，$ 2$，$ 5 (12$分$) $
  丙：$2$，$ 3$，$ 3$，$ 2 ($最多$)$
  丁：$1$，$ 1$，$ 1$，$ 1$
  丙最多：$2+3+3+2=10 ($分$)$

3. 不大于$ 2026 $可表示为$ M $的平方减$ N $的平方（其中$ M$、$N $均为非零自然数）的正整数的和为$ \underline{\quad \quad} $。

• $1539248$
• $a^2 – b^2 = (a+b)(a-b)$，$a+b$与$a-b$奇偶性相同，$a^2 – b^2$为奇数或$4$的倍数，$1 = 1^2 – 0^2 $，$4 = 2^2 – 0^2$，要排除
  总和：$1+2+\dots+2026 – (2+6+10+\dots+2026) – 1 – 4 = 1539248$

4. 将$ 1\sim7 $这$ 7 $个自然数分成两组，每组的数不重复（比如$ {167} {2345} $和$ {176} {2345} $算作同一组）两组的数和是相同的组合，占所有组合的$ \underline{\quad \quad} $。（填分数）

• $\dfrac{4}{63}$
• $1+6$，$ 2+5$，$ 3+4$
  总：$C_7^1 + C_7^2 + C_7^3 = 63 ($组$)$
  符合：$1+2+\dots+7 = 28$
  $28 \div 2 = 14$
  $14 = 7+6+1 = 7+5+2 = 7+4+3 = 6+5+3 \to 4 ($组$)$
  占$\dfrac{4}{63} $

5. $2025 $位同学编号依次是$ 1$~$2025$，围成一圈轮流报数，$1212…$报数，$1 $留下，$2 $走掉。那么最后留下的编号是$ \underline{\quad \quad} $。

• $2003$
• 变成$ 2^n$，$2025-1024=1001$，走掉了$2$、$4$、$\cdots $、$2002$，留下$2003$

6. 沃伦小区要买甲、乙两种充电桩，甲的单价比乙少$ 2 $万元，用$ 24 $万元买甲型和用$ 40 $万元买乙型数量相同，现在要购买$ 40 $个充电桩，总花费不超过$ 300 $万元，且乙型数量至少是甲型的$ 1.2 $倍，那么最少花$ \underline{\quad \quad} $万元。

• $164$
• “数量相同”$ \to $总价与单价成正比
  甲单价$ : $乙单价$ = 24 : 40 = 3 : 5$
  一份：$2 \div (5-3) = 1 ($万元$)$
  甲：$1 \times 3 = 3 ($万元$)$
  乙：$1 \times 5 = 5 ($万元$)$
  甲最多：$\left[\dfrac{40}{1+1.2}\right] = 18 ($个$)$
  最少：$18 \times 3 + (40-18) \times 5 = 164 ($万元$)$

7. 一个正整数$ N$，它的规范分解质因数为$ q_1^{a_1} \times q_2^{a_2} \times \dots \times q_n^{a_n}$，将正整数$ N $所有的因数相乘，得到$ N $的$ 15 $次方，那么$ a_1 + a_2 + \dots + a_n$的最大值是$ \underline{\quad \quad} $。

• $29$
• $N$的所有因数积为$N^{因数个数/2} $，所以$N$有$ 15 \times 2 = 30$个因数个数，
  $\Box^{29}$，$ \Box^{14} \times \Box$，$ \Box^9 \times \Box^2$，$ \Box^5 \times \Box^4$，$ \Box^4 \times \Box^2 \times \Box^1$
  最大：$29$

8. 将$ 3 $个一样的红球，$4 $个一样的蓝球，$5 $个一样的绿球分给$ 12 $个人，其中甲、乙必须拿颜色一样的，丙必须拿绿球，共有$ \underline{\quad \quad} $种拿法。

• $3150$
• ① 同拿红：$3-2=1 ($个$) \to C_9^1 C_8^4$
  ② 同拿蓝：$4-2=2 ($个$) \to C_9^3 C_6^2$
  ③ 同拿绿：$4-2=2 ($个$) \to C_9^3 C_6^4 ($注：丙已拿绿，故绿剩$ 5-1=4$，甲乙再拿$2$个绿，剩$2$个绿$)$
  共：$3150 $种

9. 如图是$ 8 \times 9 $的长方形，每个小正方形边长为$ 1$，那么图中正方形共有$ \underline{\quad \quad} $个。
   

• $240$
• $9 \times 8 + 8 \times 7 + 7 \times 6 + 6 \times 5 + 5 \times 4 + 4 \times 3 + 3 \times 2 + 2 \times 1$
  $= (8 \times 9 \times 10 – 0 \times 1 \times 2) \times \dfrac{1}{3}$
  $= 240$

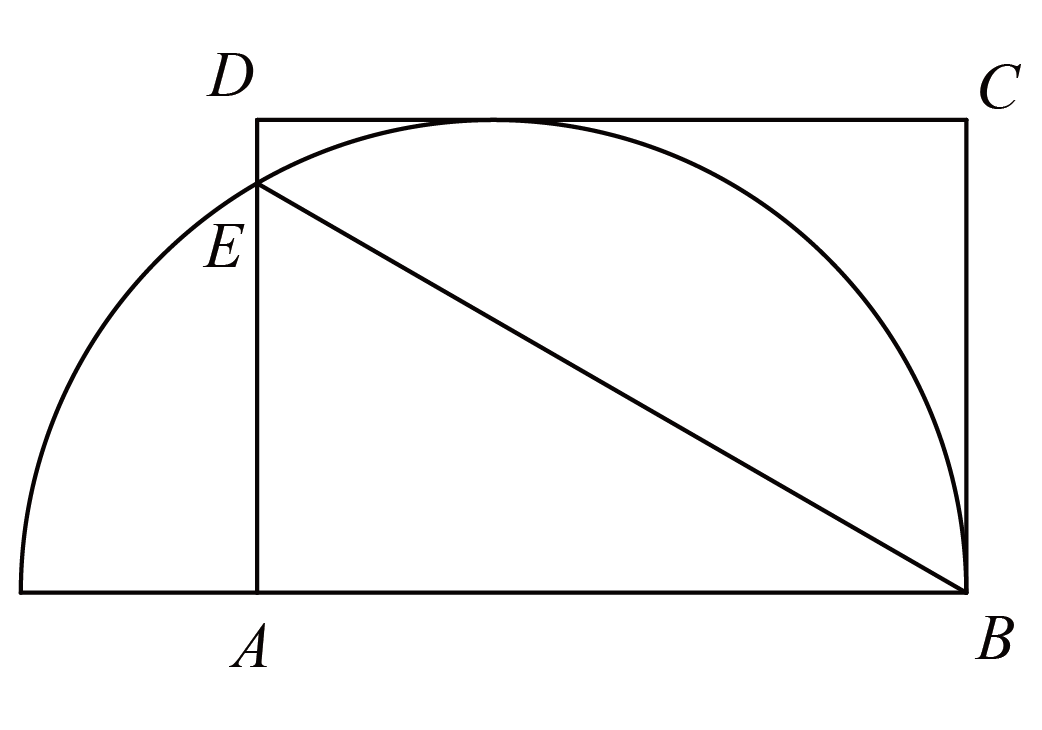
10. 如图$ 1$，有一个半径为$ 1 $的半圆，设其周长为$ l_1$；然后在左下角挖掉一个半径为$ \dfrac{1}{2} $的半圆，得到图$ 2$，设其周长为$ l_2$；接下来每次都在最小的半圆的右边挖掉一个半圆，半径是左边半圆的$ \dfrac{1}{2}$。第$ n $个图周长为$ l_n$。那么$ l_{10} = \underline{\quad \quad} $。（$\pi $取$ 3$，结果用假分数表示）
    

• $\dfrac{3071}{512}$
• 第$10$个最小半径：$\dfrac{1}{2^9} = \dfrac{1}{512}$
  $\dfrac{1}{2} \pi \times 2 \times \left(1 + \dfrac{1}{2} + \dfrac{1}{4} + \dfrac{1}{8} + \dots + \dfrac{1}{512} \right ) + \dfrac{2}{512}$
  $= 3 \times (2 – \dfrac{1}{512}) + \dfrac{2}{512}$
  $= \dfrac{3071}{512}$

11. 一个班级总共有$ 45 $个人。在$ 2025 $年，每个人都至少看了《哪吒闹海$ 2$》、《唐探$ 1900$》、《熊出没》这三部电影中的其中一部。只看了《哪吒闹海$ 2$》的有$ 24 $人，只看了《唐探$ 1900$》的有$ 6 $人，只看了《熊出没》的有$ 8 $人；看了《哪吒闹海$ 2$》的有$ 30 $人，看了《熊出没》的有$ 13 $人，三个都看的有$ 1 $人。那么同时并只看了《哪吒闹海$ 2$》和《熊出没》的有$ \underline{\quad \quad} $个人。

• $3$
• 如图
  
  $a+b = 30-24-1 = 5 ($人$)$
  $b+c = 13-8-1 = 4 ($人$)$
  $a+b+c = 45 – 24 – 8 – 6 – 1 = 6 ($人$)$
  $a: 6-4=2 ($人$)$
  $b: 5-2=3 ($人$)$

12. 一个凸六边形，每个内角都相等，已知$ AF=335$，$ BC=299$，$ CD=294$，$ DE=278$，那么这个凸六边形的周长为$ \underline{\quad \quad} $。
    

• $1071$
• 内角和：$(6-2) \times 180^\circ = 720^\circ$
  一个内角：$720^\circ \div 6 = 120^\circ \to 60^\circ ($外角$)$
  补成大等边三角形计算
  $a + 299 + 294 = b + 278 + 294 = a + b + 335$
  $a = 278 + 294 – 335 = 237$
  $b = 299 + 294 – 335 = 258$
  周长：$299 + 294 + 278 + 258 + 335 + 237 = 1701$
  

二、解答题（共 6 题，每题 20 分，共 120 分）

13. 以$ [x] $表示不超过$ x $的最大整数，若要$ \left[\dfrac{1}{17}\right ] + \left[\dfrac{2}{17}\right] + \left[\dfrac{3}{17}\right] + \dots + \left[\dfrac{n}{17}\right] \ge 2025$，则自然数$ n $的最小值是多少？

• $270$
• ①$ 17$个一周期：
  $\left[\dfrac{1}{17}\right]$，$\left[\dfrac{2}{17}\right] \dots \left[\dfrac{16}{17}\right] $值为$0 (16$个$)$
  $\left[\dfrac{17}{17}\right]$，$\left[\dfrac{18}{17}\right] \dots \left[\dfrac{33}{17}\right] $值为$1 (17$个$)$
  ② 估算：$17 \times (0+1+2+3+\dots+k) \ge 2025$
  $17 \times (0+1+\dots+15) = 2040$
  $2040 – 2025 = 15$。最多再减掉一个$ 15$。
  最少取：$16 + 17 \times 15 – 1 = 270 ($个$)$
  $n_{min} = 270$

14. 正六边形$ ABCDEF $的面积是$ 2025$，中间有两个等腰直角三角形$ \triangle EFG $和$ \triangle DCH$。那么等腰梯形的面积是多少？
    

• $675$
• 如图，延长$ BF$，$ DE $交于$ M$，设$ EF=a$，$ EN=t$
  
  $\because \angle M = 30^\circ \therefore ME = 2EF = 2a$
  $DF^2 = MF^2 = ME^2 – EF^2 = 3a^2 = 3FG^2$
  $\because EP^2 + PF^2 = PE^2$，$ PE = 2PF$
  $\therefore EF^2 = 3PF^2$，$ GF^2 = EF^2 = 3PF^2$
  $\therefore \dfrac{DN^2}{EN^2} = \dfrac{BG^2}{GP^2} = \dfrac{(BF-FG)^2}{(FG-EP)^2} = 3$
  即$ (a-t)^2 = 3t^2$
  $S_{梯形} = DN \cdot GN = \dfrac{a-t}{a} \cdot DE \cdot \dfrac{2a+t}{3a} \cdot BD$
  $= \dfrac{2}{3} S_{六} \times \dfrac{(a-t)(2a+t)}{3a^2} = \dfrac{2}{3} S_{六} \times \dfrac{1}{2} = 675$

15. 有两个大于$ 50 $的任意的质数$ p $和$ q$，那么$ p^2 – 25 $和$ q^2 – 25 $的最大公约数的最小值是多少？请给出理由。

• $24$
• $k^2 – 25 = (k-5)(k+5)$
  ①$ k \div 4 $余$ 1 $或$ 3$。$(k-5) $与$ (k+5)$
  必有一个是$ 4 $的倍数，另一个是$ 2 $的倍数
  $8 \mid (k^2-25)$
  ②$ k \div 3 $余$ 1 $或$ 2$。$(k-5) $与$ (k+5) $中
  必有一个是$ 3 $的倍数
  $3 \mid (k^2-25)$
  ③$ p^2-25 $与$ q^2-25 $必有公因数$ 24$
  $p $取$ 73$，$ q $取$ 79 $时，最大公因数为$ 24$
  故最小值为$ 24$

  答案： 24

16. 如图，三个同心圆中甲、乙、丙分别在内圈、中圈和外圈，甲从$ A$，乙从$ B$，丙从$ C $顺时针出发。甲跑一圈$ 15 $分钟，乙跑一圈$ 20 $分钟，丙跑一圈$ 25 $分钟，那么$ 10 $个小时内$ 2 $人或者$ 3 $人与圆心成一条直线（含反向成直线，出发时不算）的次数是多少？
    

• $56$
• 每各走$ \dfrac{1}{2} $圈，成一次直线。
  甲、乙：$\dfrac{1}{2} \div \left(\dfrac{1}{15} – \dfrac{1}{20}\right ) = 30 (min)$
  甲、丙：$\dfrac{1}{2} \div \left(\dfrac{1}{15} – \dfrac{1}{25}\right) = 18.75 (min)$
  乙、丙：$\dfrac{1}{2} \div \left(\dfrac{1}{20} – \dfrac{1}{25}\right) = 50 (min)$
  甲、乙、丙：$[30$，$ 50] = 150 (min)$
  共$ \dfrac{600}{30} + \dfrac{600}{18.75} + \dfrac{600}{50} – \dfrac{600}{150} \times 2 = 56 ($次$)$

17. 将自然数$ 1$、$2$、$…$、$2024 $写成一个多位数$ A=123…20232024$，那么$ A $除以$ 66 $的余数是多少？

• $24$
• $66 = 2 \times 3 \times 11$
  $A \equiv 4 \equiv 0 \pmod 2$
  $A \equiv 1+2+\dots+2024 = 2025 \times 1012 \equiv 0 \pmod 3$
  $A \equiv (2024+\dots+1000) + (999-998+997-996+\dots+101-100)$
  $ + (99+98+97+\dots+10) + (9-8+7-6+5-4+3-2+1)$
  $\equiv 1512 \times 1025 + 450 + 109 \times 45 + 5$
  $\equiv 5 \times 2 + 10 + 10 + 5$
  $\equiv 2 \pmod{11}$
  满足$ 2$、$3$、$11 $的余数的数为 “$24$”
  $A \equiv 24 \pmod{66}$

18. 一个正四面体，连接它四个面的重心，得出一个小正四面体，$8 $个顶点，每个顶点涂红色或蓝色（旋转或翻转相同视为同一种）。那么共有多少种染色方法？
    

• $35$
• ① 外围$ 4 $红：内部$ 4$红$(1$种$) 3$红$(1$种$) 2$红$(1$种$) 1$红$(1$种$) 0$红$(1$种$) – 5$种
  ② 外围$ 3 $红：内部$ 4$红$(1$种$) 3$红$(2$种$) 2$红$(2$种$) 1$红$(2$种$) 0$红$(1$种$) – $共$8$种
  ③ 外围$ 2 $红：内部$ 4$红$(1$种$) 3$红$(2$种$) 2$红$(3$种$) 1$红$(2$种$) 0$红$(1$种$) – $共$9$种
  ④ 外围$ 1 $红与$ 3 $红相同，$0 $红与$ 4 $红相同
  共：$5 \times 2 + 8 \times 2 + 9 = 35 ($种$)$