【小奥】问题59 一道几何题，小学和初中的思路都可做

问题

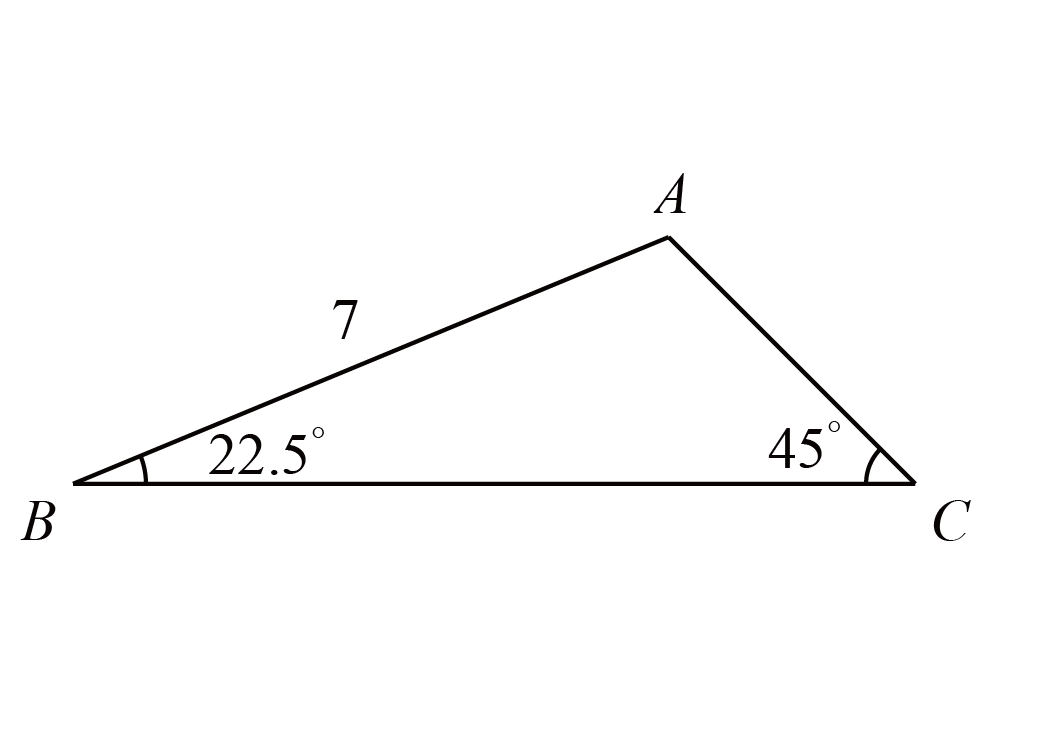
如图，$\triangle ABC$中，$AB=7$，$\angle B=22.5^{\circ}$，$\angle C=45^{\circ}$，求$\triangle ABC$的面积。

法1:小学解法

如图，将$\triangle ABC$沿着$BC$对称得到$\triangle BWC$，过$C$作$CP$平行$AW$，且$CP=AC$，连接$AW$、$WC$、$WP$

易得$$\angle ABW=45^{\circ}，\angle ACW=90^{\circ}，\angle BCP=90^{\circ}$$

那么$$AC=WC=CP$$

又$$\angle ACP=45^{\circ}+90^{\circ}=135^{\circ}$$

所以$$\angle PAC=\angle APC=22.5^{\circ}$$

那么$$\angle BAP=180^{\circ}-22.5^{\circ}-45^{\circ}-22.5^{\circ}=90^{\circ}$$

$$\angle APB=\angle WPC-22.5^{\circ}=45^{\circ}$$

所以$S_{\triangle ABC}=\dfrac{1}{2}S_{ABWC}=\dfrac{1}{2}S_{\triangle ABP}=\dfrac{1}{2}\times \dfrac{1}{2}\times 7^2=\dfrac{49}{4}$

法2:初中解法

如图，构造等腰三角形$\triangle ABW$，使得$AW=BW$，则$\angle AWB=22.5^{\circ}\times 2=45^{\circ}$

那么$\triangle AWC$是等腰直角三角形，过$A$作$AP$垂直$BC$于$P$，设$AP=x$，易得

$$WP=PC=AP=x, BW = AW =\sqrt{2}x$$

由勾股定理可得

$$AP^2+BP^2=AB^2$$

所以$$x^2 + [(\sqrt{2}+1)x]^2=7^2$$

那么$$x^2 = \dfrac{49}{4+2\sqrt{2}}$$

因此$$S_{\triangle ABC}=\dfrac{1}{2}BC\times AP=\dfrac{(\sqrt{2}+2)}{2}x^2=\dfrac{49}{4}$$