题目

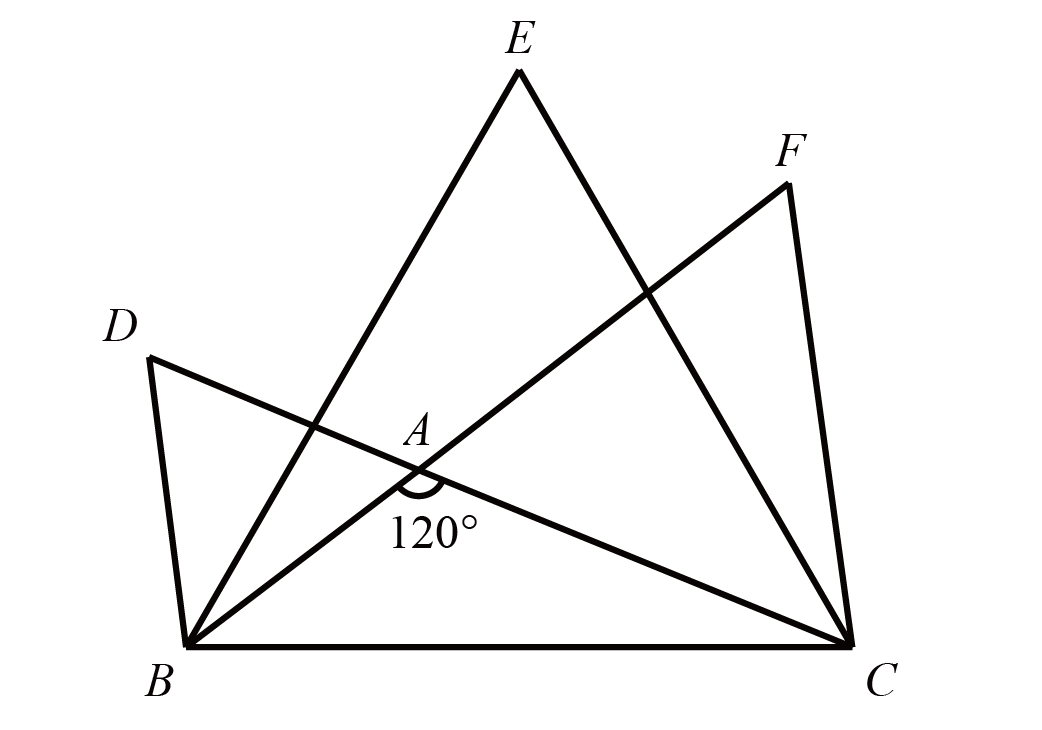
如图，$\triangle ABC$中，$\angle BAC=120^{\circ}$，$\triangle ABD$、$\triangle ACF$、$\triangle BCE$是正三角形，且$S_{\triangle ABD}=169\mathrm{cm}^2$，$S_{\triangle ACF}=361\mathrm{cm}^2$，求$S_{\triangle BCE}$

解答

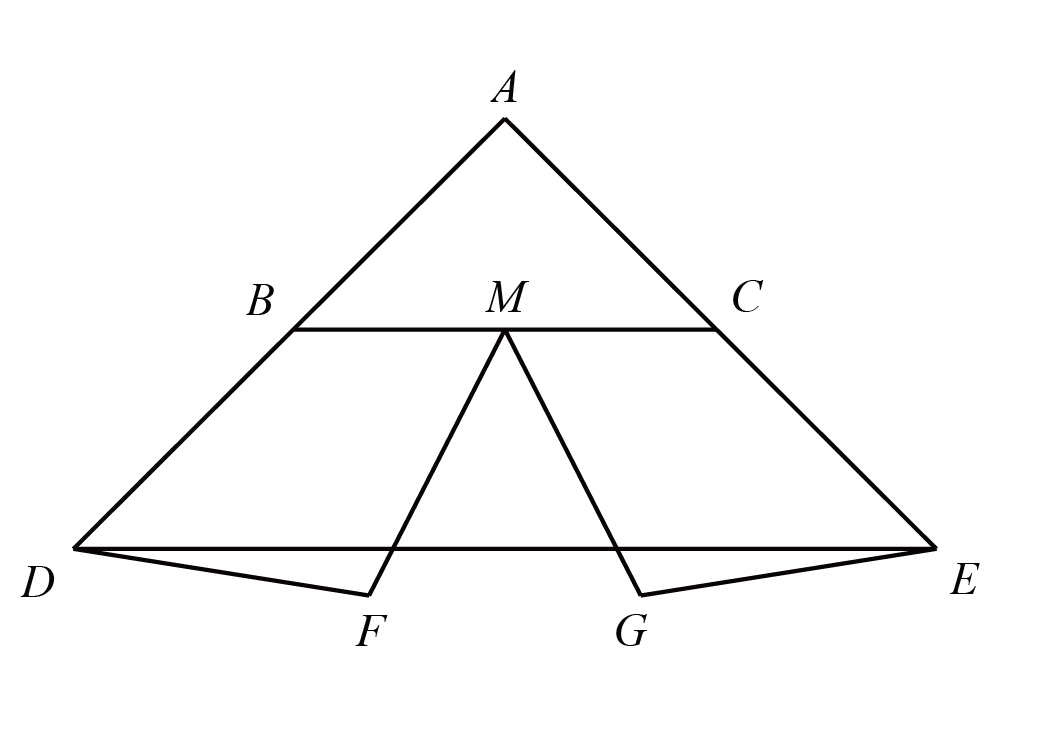
如图，构造三角弦图

$169=13\times 13$，$361=19\times 19$，$AB:AC=13:19$

则$S_{\triangle ABC}=13\times 19 =247\mathrm{cm}^2$，$S_{\triangle AXY}=6\times 6 =36\mathrm{cm}^2$

故$S_{\triangle BCE} =247 \times 3 + 36=777 \mathrm{cm}^2$