【小奥】问题32 直角梯形求面积

问题

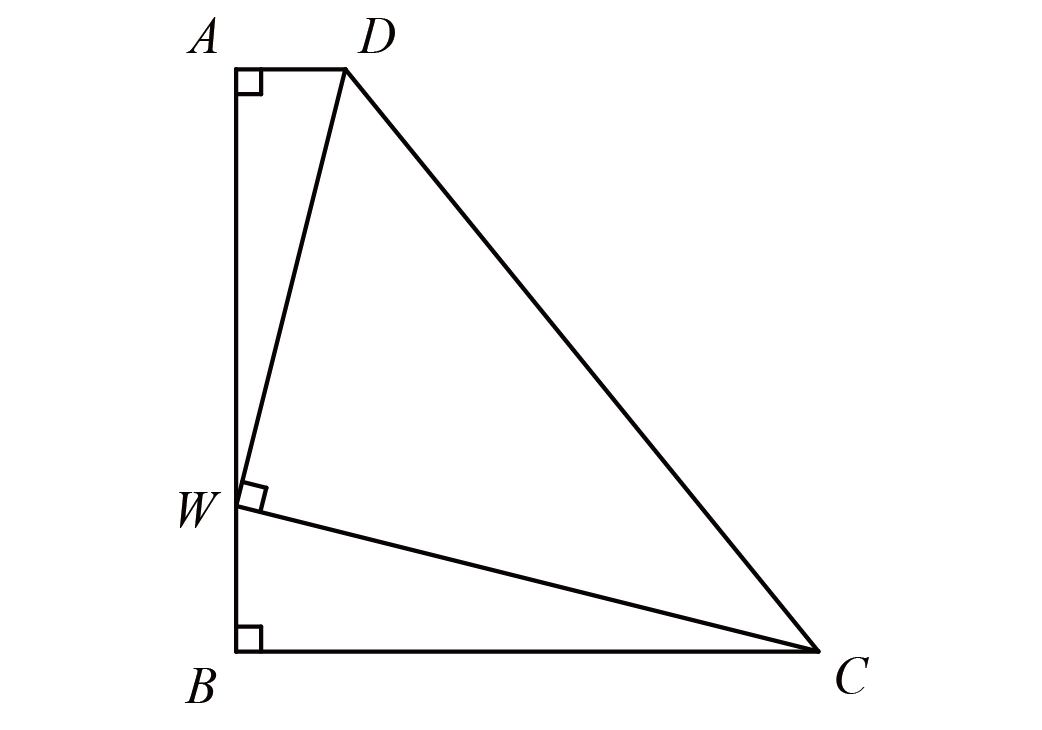
如图，一个直角梯形$ABCD$中，$AD$和$BC$平行，$AB=BC$，$\angle A=\angle B =\angle DWC=90^{\circ}$，$DW=3$，$WC=4$，求梯形$ABCD$的面积．

解析

如图，构造半个弦图，则$WE=WC=4$，$EF=WB$，$WF=BC$，又$AB=BC$，所以$AF=WB$，因为$AD$和$EF$平行，所以

$$WA:WF=WD:WE=AD:EF=3:4$$

设$AF=WB=EF=x$，则$BC=WF=4x$，$AD=\dfrac{3}{4}x$，在直角三角形$WBC$中，根据勾股定理可得

$$x^{2}+(4x)^{2}=4^{2}$$

解得$x^{2}=\dfrac{16}{17}$，那么梯形$ABCD$的面积为

$$(\dfrac{3}{4}x+4x)\times 4x \div 2=\dfrac{19}{2}x^{2}=\dfrac{152}{17}$$